本试题 “盒子中有5个球,其中3个白球,2个黑球,从中任取两个球,求取出白球的期望和方差。” 主要考查您对离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量的期望与方差
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称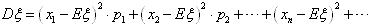 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,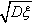 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)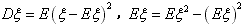 ;
;
(2)若η=aξ+b,则 ;
;
(3)若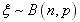 ,则
,则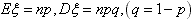 ;
;
(4)若ξ服从几何分布,则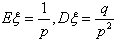 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式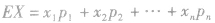 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“盒子中有5个球,其中3个白球,2个黑球,从中任取两个球,求取...”考查相似的试题有:
- 设15个同类型的零件中有2个次品,每次任取1个,共取3次,并且每次取出后不再放回.若以X表示取出次品的个数.(I)求X的分布...
- 甲、乙两人分别独立参加某高校自主招生面试,若甲、乙能通过面试的概率分别是23和34,则面试结束后通过的人数ξ的数学期望Eξ是...
- 从集合的所有非空子集中,等可能地取出一个.①记性质:集合中的所有元素之和为10,求所取出的非空子集满足性质的概率;②记所取...
- 在篮球比赛中,罚球命中1次得1分,不中得0分,如果运动员甲罚球命中的概率是0.8,记运动员甲罚球1次的得分为X,则E(X)等于( ...
- 随机变量ξ的分布列如右表所示,则Eξ=______;ξ-101Pm21-1.4m0.4
- “石头、剪刀、布”是一种广泛流传于我国民间的古老游戏,其规则是:用三种不同的手势分别表示石头、剪刀、布;两个玩家同时出...
- 口袋中有3个白球,4个红球,每次从口袋中任取一球,如果取到红球,那么继续取球,如果取到白球,就停止取球,记取球的次数为X...
- 设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计)。(1)求方程x2+bx+c=0...
- 甲、乙两人独立解出某一道数学题的概率相同,已知该题被甲或乙解出的概率为0.36. 求:(12分)(1)甲独立解出该题的概率;(2)解...
- 甲、乙两工人在一天生产中出现废品数分别是两个随机变量ξ、η,其分布列分别为:ξ0123P0.40.30.20.1η012P0.30.50.2若甲、乙两...