本试题 “(1)证明:不论为何值时,直线和圆恒相交于两点;(2)求直线被圆截得的弦长最小时的方程.” 主要考查您对点到直线的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点到直线的距离
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: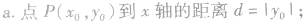
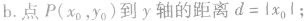
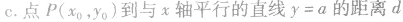

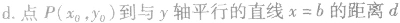
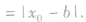
发现相似题
与“(1)证明:不论为何值时,直线和圆恒相交于两点;(2)求直...”考查相似的试题有:
- 过点P(3,6)的直线截得的弦AB的长为8,求直线
- (1)证明不论取何值,直线与圆恒交于两点; (2)求直线被圆截得的弦长最短时的方程和最短弦长
- 过点(-1,3)且与直线x-2y+3=0平行的直线方程为 .
- 圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离的最大值是______.
- (本小题满分14分)已知直线:与圆:相交于、两点,点满足.(Ⅰ)当时,求实数的值;(Ⅱ)当时,求实数的取值范围;(Ⅲ)设、是...
- 若直线y="x+b" 与曲线恰有一个公共点,则b的取值范围为______
- 求经过两点,且圆心在轴上的圆的方程.
- 将一颗质地均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6)先后抛两次,将得到的点数分别记为a,b.(1)求满足条件...
- 已知直线被圆所截得的弦长为2,则的值为 .
- 圆x2+y2-2x+4y+3=0的圆心到直线x-y=1的距离为______.