本试题 “已知点A、点B在x轴上，分别以A、B为圆心的两圆相交于M（a，5），N（9，6），则a+b的值为[ ]A.14B.-14C.-4D.4” 主要考查您对用坐标表示轴对称
圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切）
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用坐标表示轴对称
- 圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切）
用坐标表示轴对称：
关于x轴对称的点的坐标的特点是：横坐标不变，纵坐标互为相反数；
关于y轴对称的点的坐标的特点是：横坐标互为相反数，纵坐标不变。
点（x, y）关于x轴对称的点的坐标为x,-y ,
点（x, y）关于y轴对称的点的坐标为-x,y。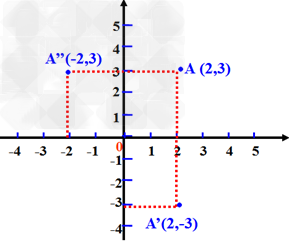
例如图中：
点A(2，3)关于x轴对称的点的坐标为A,,(-2，3);
点A(2，3)关于x轴对称的点的坐标为A,(2，3)。
点拨：
①写出平面坐标系中一个点关于x轴和y轴对称的点的坐标：
关于x轴对称的点横坐标相等,纵坐标互为相反数；关于y轴对称的点横坐标互为相反数,纵坐标相等。
②画出一个图形关于x轴或y轴对称：
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形。
圆和圆的位置关系：
如果两个圆没有公共点，那么就说这两个圆相离，相离分为外离和内含两种。
如果两个圆只有一个公共点，那么就说这两个圆相切，相切分为外切和内切两种。
如果两个圆有两个公共点，那么就说这两个圆相交。
圆心距：两圆圆心的距离叫做两圆的圆心距。
如果两个圆没有公共点，那么就说这两个圆相离，相离分为外离和内含两种。
如果两个圆只有一个公共点，那么就说这两个圆相切，相切分为外切和内切两种。
如果两个圆有两个公共点，那么就说这两个圆相交。
圆心距：两圆圆心的距离叫做两圆的圆心距。
圆和圆位置关系的性质与判定：
设两圆的半径分别为R和r，圆心距为d，那么
两圆外离
d>R+r（没有交点）
两圆外切
d=R+r （有一个交点，叫切点）
两圆相交
R-r<d<R+r（R≥r）(有两个交点)
两圆内切
d=R-r（R>r） (有一个交点,叫切点)
两圆内含
d<R-r（R>r）(没有交点)
两圆相切的性质：
（1）连心线：两圆圆心的连线。
（2）两圆相切的性质：相切两圆的连心线必过切点，即两圆圆心、切点三点在一条直线上。
发现相似题
与“已知点A、点B在x轴上，分别以A、B为圆心的两圆相交于M（a，5...”考查相似的试题有：
- 点P（2，-1）关于x轴对称的点P′的坐标是______．
- 已知A点的坐标为（-4，2），A与A′关于直线y=2对称，那么点A′的坐标为______．
- 点P（-2，3）关于x轴对称点的坐标是[ ]A．（-3，2）B．（2，-3）C．（-2，-3）D．（2，3）
- 已知在平面直角坐标系中△ABC与△DEF关于y轴对称，△HMN与△DEF关于x轴对称，则△ABC与△HMN的关系是（ ）。
- 点P（﹣1，2）关于y轴对称的点的坐标是[ ]A．（1，2）B．（﹣1，2）C．（1，﹣2）D．（﹣1，﹣2）
- 在平面直角坐标系中，点P（2，3）关于y轴的对称点在[ ]A．第一象限B．第二象限C．第三象限D．第四象限
- 如果点P（4，-5）和点Q（a，b）关于y轴对称，则a的值为（ ）。
- 已知⊙O1和⊙O2的半径分别是一元二次方程（x - 1）（x - 2）=0的两根，且O1O2=2，则⊙O1和⊙O2的位置关系是[ ]A．相交B．外切C．...
- 已知⊙O1与⊙O2内切，O1O2=6cm，⊙O1的半径为8cm，则⊙O2的半径为（ ）cm。
- 已知⊙O1和⊙O2的半径分别为3和4，圆心距OlO2=7，则这两圆的位置关系是（ ）A．相离B．外切C．相交D．内切