本试题 “设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式1a1a2+1a2a3+…+1anan+1=kn+ba1an+1对任意n(n∈N*)恒...” 主要考查您对数列求和的其他方法(倒序相加,错位相减,裂项相加等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 数列求和的其他方法(倒序相加,错位相减,裂项相加等)
数列求和的常用方法:
1.裂项相加法:数列中的项形如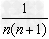 的形式,可以把
的形式,可以把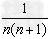 表示为
表示为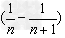 ,累加时抵消中间的许多项,从而求得数列的和;
,累加时抵消中间的许多项,从而求得数列的和;
2、错位相减法:源于等比数列前n项和公式的推导,对于形如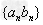 的数列,其中
的数列,其中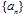 为等差数列,
为等差数列,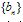 为等比数列,均可用此法;
为等比数列,均可用此法;
3、倒序相加法:此方法源于等差数列前n项和公式的推导,目的在于利用与首末两项等距离的两项相加有公因式可提取,以便化简后求和。
4、分组转化法:把数列的每一项分成两项,或把数列的项“集”在一块重新组合,或把整个数列分成两个部分,使其转化为等差或等比数列,这一求和方法称为分组转化法。
5、公式法求和:所给数列的通项是关于n的多项式,此时求和可采用公式求和,常用的公式有:
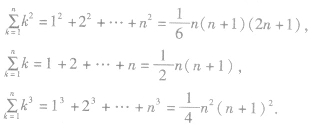
数列求和的方法多种多样,要视具体情形选用合适方法。
数列求和特别提醒:
(1)对通项公式含有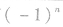 的一类数列,在求
的一类数列,在求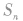 时,要注意讨论n的奇偶性;
时,要注意讨论n的奇偶性;
(2)在用等比数列前n项和公式时,一定要分q=1和q≠1两种情况来讨论。
发现相似题
与“设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命...”考查相似的试题有:
- 求和 .
- 求数列1,312,514,…(2n-1)+12n-1…的前n项和.
- 数列,…前n项的和为A.B.C.D.
- 数列的前项和为_____________.
- 已知数列an中,a1=1,a2=a-1(a≠1,a为实常数),前n项和Sn恒为正值,且当n≥2时,1Sn=1an-1an+1.(1)求证:数列Sn是等比数...
- (15分)已知是数列的前项和,(,),且.(1)求的值,并写出和的关系式;(2)求数列的通项公式及的表达式;(3)我们可以...
- 无穷等比数列{an}中,a1+a2=3(a3+a4)≠0,a5=1,则limn→∞(a1+a3+…+a2n-1)=______.
- 等差数列{an}中,a1、a2、a3分别是下表第一、二、三列中的某个数,且a1、a2、a3中的任何两个数不在下表的同一行.(Ⅰ)求数列...
- 已知等比数列{an}各项都是正数,a1=3,a1+a2+a3=21,Sn为{an}的前n项和,(Ⅰ)求通项an及Sn;(Ⅱ)设{bn-an}是首项为1,公差...
- 已知等差数列{an}前三项和为-3,前三项积为8(I)求等差数列{an}的通项公式;(II)若a2,a3,a1成等比数列,求数列{1anan+1}...