位似图形：
如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，那么这两个图形叫做位似图形。位似图形对应点连线的交点是位似中心，这时的相似比又称为位似比。
注：
①位似图形是相似图形的特例；
②位似图形一定是相似图形，但相似图形不一定是位似图形；
③位似图形的对应边互相平行或共线。

位似图形的性质：
位似图形的任意一对对应点与位似中心在同一直线上，它们到位似中心的距离之比等于相似比。 
1.位似图形对应线段的比等于相似比。
2.位似图形的对应角都相等。
3.位似图形对应点连线的交点是位似中心。
4.位似图形面积的比等于相似比的平方。
5.位似图形高、周长的比都等于相似比。
6.位似图形对应边互相平行或在同一直线上。

位似图形作用：
利用位似可以将一个图形任意放大或缩小。
位似图形的中心可以在任意的一点，不过位似图形也会随着位似中心的位变而位变。
根据一个位似中心可以作两个关于已知图形一定位似比的位似图形,这两个图形分布在位似中心的两侧,并且关于位似中心对称。
作图步骤：（位似比，即位似图形的相似比，指的是要求画的新图形与参照的原图形的相似比）
①首先确定位似中心，位似中心的位置可随意选择；
②确定原图形的关键点，如四边形有四个关键点，即它的四个顶点；
③确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小；
④符合要求的图形不惟一，因为所作的图形与所确定的位似中心的位置有关，并且同一个位似中心的两侧各有一个符合要求的图形，最好做两个。

位似变换：
把一个几何图形变换成与之位似的图形,叫做位似变换。
物理中的透镜成像就是一种位似变换,位似中心为光心。
位似变换应用极为广泛，特别是可以证明三点共线等问题。

点的坐标的概念：
点的坐标用（a，b）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对，当a≠b时，（a，b）和（b，a）是两个不同点的坐标。
各象限内点的坐标的特征 ：
点P(x，y)在第一象限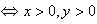；点P(x，y)在第二象限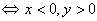
点P(x，y)在第三象限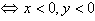；点P(x，y)在第四象限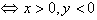

坐标轴上的点的特征：
点P(x，y)在x轴上y=0，x为任意实数
点P(x，y)在y轴上x=0，y为任意实数
点P(x，y)既在x轴上，又在y轴上x，y同时为零，即点P坐标为（0，0）。

点P(x，y)到坐标轴及原点的距离：
（1）点P(x，y)到x轴的距离等于|y|；
（2）点P(x，y)到y轴的距离等于|x|；
（3）点P(x，y)到原点的距离等于。
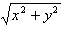坐标表示位置步骤：
利用平面直角坐标系绘制区域内一些地点分布情况的平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确定X轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。

定义：
将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。平移是图形变换的一种基本形式。平移不改变图形的形状和大小，平移可以不是水平的。

平移基本性质：
经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等；
平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
（1）图形平移前后的形状和大小没有变化，只是位置发生变化;
（2）图形平移后，对应点连成的线段平行（或在同一直线上）且相等
（3）多次连续平移相当于一次平移。
（4）偶数次对称后的图形等于平移后的图形。
（5）平移是由方向和距离决定的。
这种将图形上的所有点都按照某个方向作相同距离的位置移动，叫做图形的平移运动，简称为平移
平移的条件：确定一个平移运动的条件是平移的方向和距离。

平移的三个要点
1 原来的图形的形状和大小和平移后的图形是全等的。
2 平移的方向。（东南西北，上下左右,东偏南n度，东偏北n度，西偏南n度，西偏北n度）
3 平移的距离。（长度，如7厘米，8毫米等）

平移作用：
1.通过简单的平移可以构造精美的图形。也就是花边，通常用于装饰，过程就是复制-平移-粘贴。
2.平移长于平行线有关,平移可以将一个角,一条线段,一个图形平移到另一个位置,是分散的条件集中到一个图形上,使问题得到解决。

平移作图的步骤：
（1）找出能表示图形的关键点；
（2）确定平移的方向和距离；
（3）按平移的方向和距离确定关键点平移后的对应点；
（4）按原图的顺序，连结各对应点。