本试题 “袋中装有2个白球,2个红球,它们大小、形状完全相同,仅强度不同,白球被击中1次破裂(成粉末),红球被击中2次破裂(被击中1次外形不改变).现随机击2次,...” 主要考查您对n次独立重复试验
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- n次独立重复试验
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
独立重复试验:
(1)独立重复试验的意义:做n次试验,如果它们是完全同样的一个试验的重复,且它们相互独立,那么这类试验叫做独立重复试验.
(2)一般地,在n次独立重复试验中,设事件A发生的次数为X,在每件试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为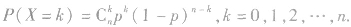 此时称随机变量X服从二项分布,记作
此时称随机变量X服从二项分布,记作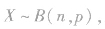 并称p为成功概率.
并称p为成功概率.
(3)独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的.
(4)独立重复试验概率公式的特点: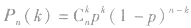 是n次独立重复试验中某 事件A恰好发生k次的概率.其中,n是重复试验的次数,p是一次试验中某事件A发生的概率,k是在n次独立重复试验中事件A恰好发生的次数,需要弄清公式中n,p,k的意义,才能正确运用公式.
是n次独立重复试验中某 事件A恰好发生k次的概率.其中,n是重复试验的次数,p是一次试验中某事件A发生的概率,k是在n次独立重复试验中事件A恰好发生的次数,需要弄清公式中n,p,k的意义,才能正确运用公式.
求独立重复试验的概率:
(1)在n次独立重复试验中,“在相同条件下”等价于各次试验的结果不会受其他试验的影响,即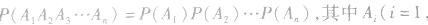 2,…,n)是第i次试验的结果.
2,…,n)是第i次试验的结果.
(2)独立重复试验是相互独立事件的特例,只要有“恰好”“恰有”字样的用独立重复试验的概率公式计算更简单,要弄清n,p,k的意义。
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称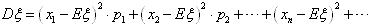 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,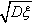 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)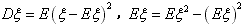 ;
;
(2)若η=aξ+b,则 ;
;
(3)若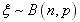 ,则
,则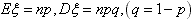 ;
;
(4)若ξ服从几何分布,则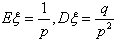 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式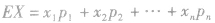 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“袋中装有2个白球,2个红球,它们大小、形状完全相同,仅强度...”考查相似的试题有:
- 某同学进行了2次投篮(假设这两次投篮互不影响),每次投中的概率都为p(p≠0),如果最多投中1次的概率不小于至少投中1次的概...
- 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶...
- 在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和...
- 设随机变量ξ的分布列为 P(ξ=k)=m()k,k=1,2,3,则m的值是( ) A. B. C. D.
- 某企业为更好地了解设备改造前后与生产合格品的关系,随机抽取了100件产品进行分析,但由于工作人员不小心,丢失了部分数据:...
- 设事件A发生的概率为p(0
- 一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号。若拿出球...
- 一个盒子装有六张卡片,上面分别写着如下六个函数:f1(x)=x3,f2(x)=5|x|,f3(x)=2,,,f6(x)=xcosx,(Ⅰ)从中任意...
- 已知随机变量X的分布列为:P(X=0)=14,P(X=1)=p,P(X=x)=14,且E(X)=1,则随机变量X的标准差V(X)等于______.
- 一个暗箱中有大小相同的3只白球和2只黑球共5只球,每次从中取出1只球,取到白球得2分,取到黑球得3分,甲从暗箱中有放回地依...