集合A={x||x|＜4}，集合B={x|＞0}，则集合A∩CRB=[ ]A．（﹣4，1]B．（4，1）C．（0，4）D．[1，4）,高中三年级,数学试题,集合间交、并、补的运算（用Venn图表示）考点,分式不等式考点,好技网

本试题 “集合A={x||x|＜4}，集合B={x|＞0}，则集合A∩CRB=[ ]A．（﹣4，1]B．（4，1）C．（0，4）D．[1，4）” 主要考查您对
集合间交、并、补的运算（用Venn图表示）

分式不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

1、交集概念：

（1）一般地，由所有属于集合A且集合B的元素所组成的集合，叫做A与B的交集，记作A∩B，读作A交B，表达式为A∩B＝｛x|x∈A且x∈B｝。
（2)韦恩图表示为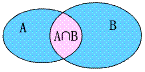
。

2、并集概念：

（1）一般地，由所有属于集合A或集合B的元素所组成的集合，叫做A与B的并集，记作A∪B，读作A并B，表达式为A∪B＝｛x|x∈A或x∈B｝。
（2）韦恩图表示为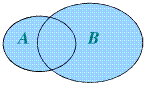
。

3、全集、补集概念：

（1）全集：一般地，如果一个集合含有我们所要研究的各个集合的全部元素，就称这个集合为全集，通常记作U。
补集：对于一个集合A，由全集U中所有不属于A的元素组成的集合称为集合A相对于全集U的补集，记作C_UA，读作U中A的补集，表达式为C_UA={x|x∈U，且x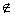A}。
（2）韦恩图表示为
。

1、交集的性质：

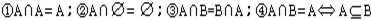
2、并集的性质：

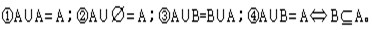
3、补集的性质：

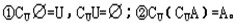
分母恒为正时可去分母；分母不恒为正时不能去分母，应先移项使右边为0再通分并将分子分母分解因式，最后用标根法求解。解分式不等式的主旨是化分式不等式为整式不等式，进行求解。

分式不等式的解法：

分母恒为正时可去分母；分母不恒为正时不能去分母，应先移项使右边为0再通分并将分子分母分解因式，最后用标根法求解。解分式不等式的主旨是化分式不等式为整式不等式，进行求解，即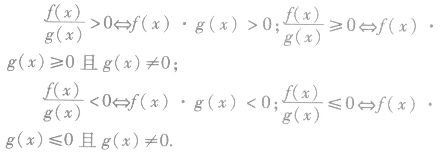

发现相似题

与“集合A={x||x|＜4}，集合B={x|＞0}，则集合A∩CRB=[ ]A．（﹣4...”考查相似的试题有：