本试题 “已知向量m=(cosx,-sinx),n=(cosx,sinx-23cosx),x∈R,令f(x)=m•n,(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)当x∈(0,π2]时,求函数f(x)的值域.” 主要考查您对正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
- 向量数量积的含义及几何意义
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 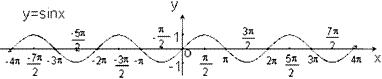
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 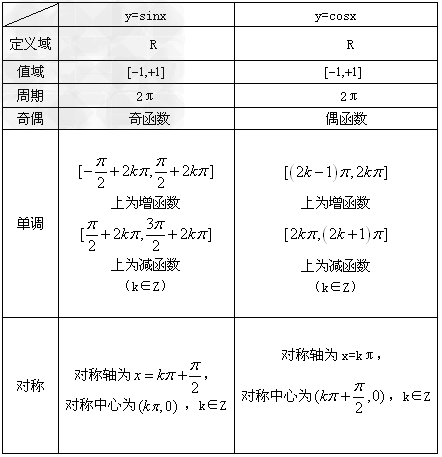
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当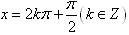 时,y取最大值1,
时,y取最大值1,
当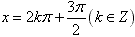 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当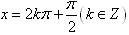 时,y取最大值1,
时,y取最大值1,
当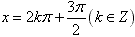 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
两个向量的夹角的定义:
对于非零向量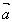 ,
,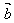 ,作
,作 称为向量
称为向量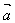 ,
,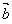 的夹角,当
的夹角,当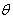 =0时,
=0时,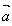 ,
,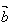 同向,当
同向,当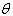 =π时,
=π时,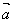 ,
,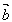 反向,
反向,
当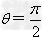 时,
时,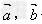 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积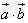 等于
等于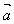 的模
的模 与
与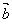 在
在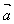 上的投影
上的投影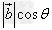 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知向量m=(cosx,-sinx),n=(cosx,sinx-23cosx),x∈R,令f...”考查相似的试题有:
- (本小题满分12分)某简谐运动得到形如的关系式,其中:振幅为4,周期为6,初相为;(Ⅰ)写出这个确定的关系式;(Ⅱ)用五点...
- 把函数y=cos(x+4π3)的图象向右平移θ(θ>0)个单位,所得的函数为偶函数,则θ的最小值为______.
- 在上的实数解的个数是( )A.98B.100C.102D.200
- (本小题10分)已知函数(1)用五点法画出它在一个周期内的闭区间上的图像;(2)指出的周期、振幅、初相、对称轴;(3)说明...
- 如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确...
- 若函数的图象(部分)如图所示,则的取值是( )A.B.C.D.
- 函数的值域是________________________.
- (本小题共12分)已知函数的部分图象如图所示,求f(x)的解析式.
- 函数f(x)=sinx-3cosx,x∈[0,π]的单调减区间为 ______.
- △ABC的外接圆的圆心为O,半径为1,且,则向量在方向上的投影为A.B.C.D.