本试题 “给出下列五个命题:①长度相等,方向不同的向量叫做相反向量;②设b,c是同一平面内的两个不共线向量,则对于平面内的任意一个向量a,有且只有一对实数λ1,λ2,...” 主要考查您对真命题、假命题
向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 向量数量积的含义及几何意义
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
两个向量的夹角的定义:
对于非零向量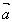 ,
,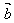 ,作
,作 称为向量
称为向量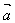 ,
,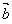 的夹角,当
的夹角,当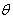 =0时,
=0时,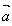 ,
,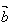 同向,当
同向,当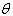 =π时,
=π时,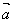 ,
,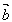 反向,
反向,
当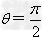 时,
时,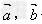 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积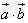 等于
等于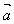 的模
的模 与
与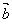 在
在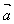 上的投影
上的投影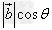 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“给出下列五个命题:①长度相等,方向不同的向量叫做相反向量;...”考查相似的试题有:
- 关于直线a,b,c以及平面M,N,给出下面命题:①若a∥M,b∥M,则a∥b②若a∥M,b⊥M,则b⊥a③若a∥M,b⊥M,且c⊥a,c⊥b,则c⊥M④若a⊥M,...
- 若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A.若α∥β,lα,nβ,则l∥nB.若α⊥β,lα,则...
- 已知a,b均为单位向量,其中夹角为θ,有下列四个命题p1:|a+b|>1⇔θ∈[0,2π3)p2:|a+b|>1⇔θ∈(2π3,π]p3:|a-b|>1⇔θ∈[0,π...
- 给出下列四个命题:①若|x-lgx|<x+|lgx|成立,则x>1;②若p=a+1a-2(a>2),q=(12)x2-2(x∈R),则p>q,③已知|a|=|b|=2,a...
- 正三角形ABC边长为2,设=2,=3,则·=________.
- 下列各组向量中, 向量a , b, c 共面的一组是 ( )A.a =" (" 4, 2, 1 ), b =" (–1," 2 , 2 ), c =" (" –1, 1 ; 5 ).B. a =" (...
- 已知,若与的夹角为锐角,则的取值范围是 。
- 已知向量、满足,则 .
- ,且,则、的夹角为 ( )A.B.C.D.
- .已知,,,则与的夹角为