（本题满分15分）已知椭圆的离心率为，椭圆上任意一点到右焦点的距离的最大值为。（I）求椭圆的方程；（II）已知点是线段上一个动点（为坐标原点,高中三年级,数学试题,椭圆的定义考点,好技网

本试题 “（本题满分15分）已知椭圆的离心率为，椭圆上任意一点到右焦点的距离的最大值为。（I）求椭圆的方程；（II）已知点是线段上一个动点（为坐标原点），是否存在...” 主要考查您对
椭圆的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

椭圆的第一定义：

平面内与两个定点为F₁，F₂的距离的和等于常数（大于）的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。特别地，当常数等于时，轨迹是线段F₁F₂，当常数小于时，无轨迹。

椭圆的第二定义：

平面内到定点F的距离和到定直线l的距离之比等于常数e（0＜e＜1）的点的轨迹，叫做椭圆，定点F叫椭圆的焦点，定直线l叫做椭圆的准线，e叫椭圆的离心率。

椭圆的定义应该包含几个要素：

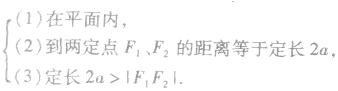
利用椭圆的定义解题：

当题目中出现一点在椭圆上的条件时，注意使用定义

发现相似题

与“（本题满分15分）已知椭圆的离心率为，椭圆上任意一点到右焦...”考查相似的试题有：