函数解析式的常用求解方法：

（1）待定系数法：（已知函数类型如：一次、二次函数、反比例函数等）：若已知f（x）的结构时，可设出含参数的表达式，再根据已知条件，列方程或方程组，从而求出待定的参数，求得f（x）的表达式。待定系数法是一种重要的数学方法，它只适用于已知所求函数的类型求其解析式。
（2）换元法（注意新元的取值范围）：已知f（g（x））的表达式，欲求f（x），我们常设t=g（x），从而求得，然后代入f（g（x））的表达式，从而得到f（t）的表达式，即为f（x）的表达式。
（3）配凑法（整体代换法）：若已知f（g（x））的表达式，欲求f（x）的表达式，用换元法有困难时，（如g（x）不存在反函数）可把g（x）看成一个整体，把右边变为由g（x）组成的式子，再换元求出f（x）的式子。
（4）消元法（如自变量互为倒数、已知f（x）为奇函数且g（x）为偶函数等）：若已知以函数为元的方程形式，若能设法构造另一个方程，组成方程组，再解这个方程组，求出函数元，称这个方法为消元法。
（5）赋值法（特殊值代入法）：在求某些函数的表达式或求某些函数值时，有时把已知条件中的某些变量赋值，使问题简单明了，从而易于求出函数的表达式。

不等式的定义：

一般地，用不等号表示不相等关系的式子叫做不等式，常见的不等号有“<”“>”“ ≤”“≥”及“≠”。

 严格不等式的定义：

用“>"“<”连接的不等式叫做严格不等式。

非严格不等式的定义：

用“≤”和“≥”连接的不等式叫做非严格不等式．
特别提醒：a=b，a>b中，只要有一个成立，就有a≥b．

不等式的性质：

（1）如果a＞b，那么b＜a；如果b＜a，那么a＞b，即a＞b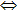b＜a；
（2）如果a＞b，b＞c，那么a＞c，即a＞b，b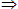＞ca＞c；
（3）如果a＞b，那么a+c＞b+c；
（4）如果a＞b，c＞0，那么ac＞bc；如果a＞b，c＜0，那么ac＜bc；
（5）如果a＞b，c＞d，那么a+c＞b+d；
（6）如果a＞b＞0，c＞d＞0，那么ac＞bd；
（7）如果a＞b＞0，那么aⁿ＞bⁿ（n∈N，n≥2）；
（8）如果a＞b＞0，那么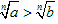（n∈N，n≥2）。

不等关系与不等式的区别：

不等关系强调的是量与量之间的关系，可以用符号“<…>…≤”“≥”来表示，也可以用语言表述；
而不等式则是用来表示不等关系的式子，可用“a>b”‘a<b”“a≥b a≤b”等式子来表示，不等关系是通过不等式来体现的．

不等式的分类：

①按成立的条件分：a．绝对不等式：不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式；b．条件不等式：不等式中的字母取某些允许值才能成立的不等式叫做条件不等式；c．矛盾不等式：不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式；
②按不等号开口方向分：a．同向不等式：不等号方向相同的两个不等式；b．异向不等式：不等号方向相反的两个不等式．

一元二次不等式的概念：

只含有一个未知数，并且未知数的最高次数是2 的不等式称为一元二次不等式．

一元二次不等式的解集：

使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解，一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集。

同解不等式：

如果两个不等式的解集相同，那么这两个不等式叫做同解不等式，如果一个不等式变形为另一个不等式时，这两个不等式是同解不等式，那么这种变形叫做不等式的同解变形。 

二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系： 

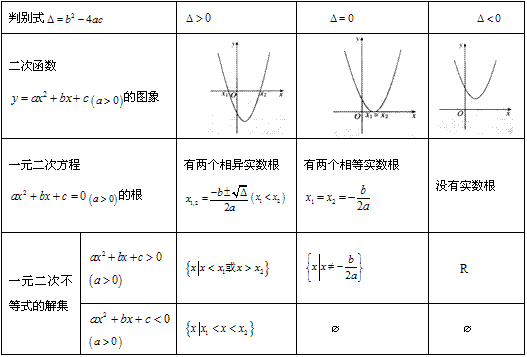
解不等式的过程：

解不等式的过程就是将不等式进行同解变形，化为最简形式的同解不等式的过程．变形时要注意条件的限制，比如：分母是否有意义，定义域是否有限制等．

解一元二次不等式的一般步骤为：

(1)对不等式变形，使一端为零且二次项系数大于零；(2)计算相应的判别式；(3)当△≥0时，求出相应的一元二次方程的根；(4)根据二次函数图象写出一元二次不等式的解集．

解含有参数的一元二次不等式：

(1)要以二次项系数与零的大小作为分类标准进行分类讨论；(2)转化为标准形式的一元二次不等式（即二次项系数大于零）后，再以判别式与零的大小作为分类标准进行分类讨论；(3)如果判别式大于零，但两根的大小还不能确定，此时再以两根的大小作为分类标准进行分类讨论。