本试题 “已知向量,,函数, 三个内角的对边分别为.(1)求的单调递增区间;(2)若,求的面积.” 主要考查您对正弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即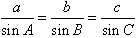 =2R。
=2R。
有以下一些变式:
(1)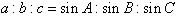 ;
;
(2)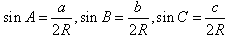 ;
;
(3)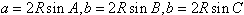 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 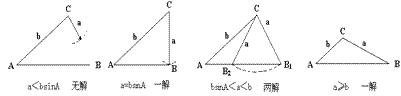
也可根据a,b的关系及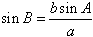 与1的大小关系来确定。
与1的大小关系来确定。
发现相似题
与“已知向量,,函数, 三个内角的对边分别为.(1)求的单调递增...”考查相似的试题有:
- (本小题满分12分)在中,分别是角A、B、C的对边,且(1)求角B的大小;(2)若,求的面积.
- 在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=acosB。(1)求角B的大小;(2)若b=3,sinC=2sinA,求a,c的值。
- 在中,角、、的对边分别为、、,且满足.(1)求角的大小;(2)当时,求的面积
- 已知锐角△ABC的面积为33,BC=4,CA=3,则角C的大小为 ______°.
- 在△ABC中,A=60°,a=,b=,则B=
- 在ABC中,已知,,,求.
- 已知函数f(x)=2-sin(2x+)-2sin2x,x∈R,记△ABC的内角A,B,C的对边长分别为a,b,c,若=1,b=1,c=,求a的值。
- 设的内角,,所对的边长分别为,,,且,.(1)当时,求的值;(2)当的面积为时,求的值.
- 设△ABC的内角A、B、C所对的边分别为a,b,c,若sinB+sinC=2sinA,3a=5c,则角B=( )A. 60 B. 90 C. 120 D.150
- ΔABC中,a=1,b=, A=30°,则B等于 ( )A.60°B.60°或120°C.30°或150°D.120°