本试题 “过点Q(-2,)作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4,(1)求r的值;(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点...” 主要考查您对基本不等式及其应用
圆的标准方程与一般方程
圆的切线方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 基本不等式及其应用
- 圆的标准方程与一般方程
- 圆的切线方程
基本不等式:
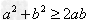 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①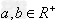 ,
,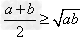 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②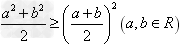 ;③
;③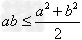 ;④
;④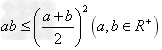 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有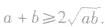
(2)基本不等式又称为均值定理、均值不等式等,其中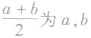 的算术平均数,
的算术平均数,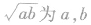 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即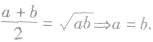
对于两个正数x,y,若已知xy,x+y,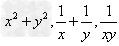 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2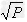 ,
,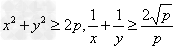 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值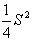 ,
,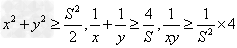 ;
;
(3)已知x2+y2=p,则x+y有最大值为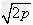 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式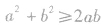 的形式可以是
的形式可以是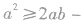
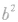 ,也可以是
,也可以是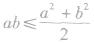 ,还可以是
,还可以是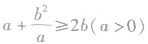 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

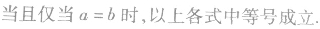
圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为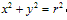 。
。
圆的一般方程:
圆的一般方程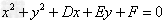
当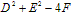 >0时,表示圆心在
>0时,表示圆心在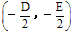 ,半径为
,半径为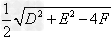 的圆;
的圆;
当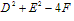 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.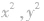 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如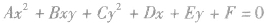 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即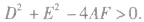
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
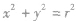 |
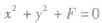 |
| 过原点 |
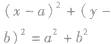 |
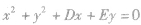 |
| 圆心在x轴上 |
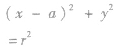 |
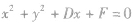 |
| 圆心在y轴上 |
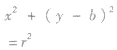 |
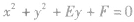 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
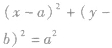 |
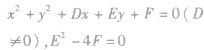 |
|
与x,y轴都相切 |
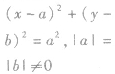 |
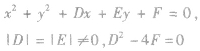 |
| 圆心在x轴上且过原点 |
 |
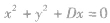 |
| 圆心在y轴上且过原点 |
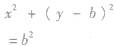 |
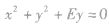 |
圆的切线方程:
1、已知圆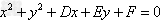 ,
,
(1)若已知切点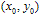 在圆上,则切线只有一条,其方程是
在圆上,则切线只有一条,其方程是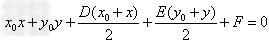 ;
;
(2)当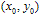 圆外时,
圆外时,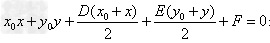 表示过两个切点的切点弦方程。
表示过两个切点的切点弦方程。
(3)过圆外一点的切线方程可设为 ,再利用相切条件求k,这时必有两条切线。
,再利用相切条件求k,这时必有两条切线。
(4)斜率为k的切线方程可设为y=kx+b,再利用相切条件求b,必有两条切线。
2、已知圆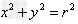 ,
,
(1)过圆上的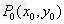 点的切线方程为
点的切线方程为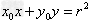 ;
;
(2)斜率为k的圆的切线方程为 。
。
圆的切线方程的求法:
①代数法:设出切线方程,利用切线与圆仅有一个交点,将直线方程代入圆的方程,从而△=0,可求解;
②几何法利用几何特征:圆心到切线的距离等于圆的半径,可求解.
过定点的圆的切线方程:
①过圆上一点的切线方程:
与圆 的切线方程是
的切线方程是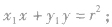
与圆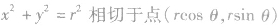 的切线方程是
的切线方程是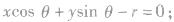
与圆 的切线方程是
的切线方程是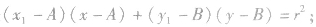
与圆 的切线方程是
的切线方程是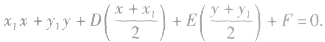
②过圆外一点的切线方程:设 外一点,求过P0点的圆的切线.
外一点,求过P0点的圆的切线.
方法l:设切点是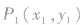 ,解方程组
,解方程组

方法2:设切线方程是
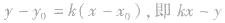
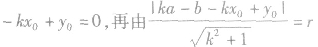 ,再由
,再由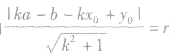 求出待定系数k,就可写出切线方程.
求出待定系数k,就可写出切线方程.特别提醒:一般说来,方法2比较简便,但应注意,可能遗漏k不存在的切线.因此,当解出的k值唯一时,应观察图形,看是否有垂直于x轴的切线.
与“过点Q(-2,)作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD...”考查相似的试题有:
- 已知a,b,c∈(0,+∞),3a-2b+c=0,则acb的( )A.最大值是3B.最小值是3C.最大值是33D.最小值是33
- 已知,使式中的、满足约束条件(1)作出可行域;(2)求z的最大值.
- 函数y=loga(x+3)-1(a>0且a≠1)的图象恒过定点A,若点A在mx+ny+2=0上,其中mn>0,则1m+ 2n的最小值为______.
- 在平面直角坐标系中,若不等式组(为常数)所表示的平面区域的面积等于2,则的值为 .
- 若a,b,c>0,且a2+ab+ac+bc=4,则2a+b+c的最小值为( )。
- 已知a,b∈R+,直线bx-ay-ab=0始终平分圆(x-1)2+(y+4)2=4,则a+b的最小值为______.
- 在平面直角坐标系中,已知圆和圆.(1)若直线经过点(2,-1)和圆的圆心,求直线的方程;(2)若点(2,-1)为圆的弦的中点,...
- 已知圆C与圆(x-1)2+y2=1关于直线y=-x+2对称,则圆C的方程为[ ]A.(x-1)2+y2=1B.(x+1)2+(y-2)2=1C.(x-2)2+(y-1)2=1D.x2+(y-...
- 已知圆通过不同的三点,,和,且该圆在点处的切线的斜率等于1,求圆的方程.
- 已知圆C:x2+y2=5,及点A(1,-2),Q(0,4).(1)求过点A的圆的切线方程;(2)如果P是圆C上一个动点,求线段PQ的中点M的...