本试题 “本题设有（1）（2）（3）三个选考题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应...” 主要考查您对绝对值不等式
简单曲线的极坐标方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 绝对值不等式
- 简单曲线的极坐标方程
绝对值不等式：
当a>0时，有
；
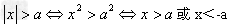或x＜-a 。
绝对值不等式的解法：
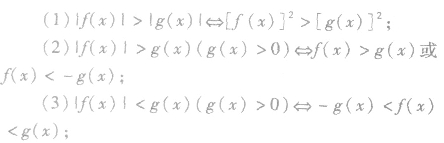
(4)含两个或两个以上绝对值符号的不等式可用零点分区间的方法去绝对值符号求解，也可以用图象法求解。
曲线的极坐标方程的定义：
一般地，在极坐标系中，如果平面曲线C上任意一点的极坐标中至少有一个满足方程f（ρ，θ）=0，并且坐标适合方程f（ρ，θ）=0的点都在曲线上，那么方程f（ρ，θ）=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法：
直译法、待定系数法、相关点法等。
圆心为（α，β）（a＞0），半径为a的圆的极坐标方程为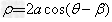
，此圆过极点O。
直线的极坐标方程：
直线的极坐标方程是ρ=1/（2cosθ＋4sinθ）。
圆的极坐标方程：
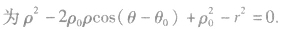
这是圆在极坐标系下的一般方程。
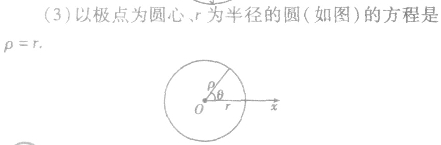
过极点且半径为r的圆方程：
发现相似题
与“本题设有（1）（2）（3）三个选考题，每题7分，请考生任选2题...”考查相似的试题有：
- 已知向量b=(3，-1)，|a|=2，则|2a-b|的最大值为______．
- 请考生在下列二题中任选一题作答。（1）如果关于的不等式的解集不是空集，则参数的取值范围是（2）直线与圆相切，则_________
- 选做题已知函数．（Ⅰ）当a=7时，求函数f(x)的定义域；（Ⅱ）若关于x的不等式f(x)≥3的解集是R，求实数a的取值范围．
- 设函数f（x）=|x-4|+|x-a|（a＜4）．（Ⅰ）若f（x）的最小值为3，求a值；（Ⅱ）求不等式f（x）≥3-x的解集．
- 解不等式|x|＜5．
- （12分）设函数f(x)=∣2x+1∣-∣x-4∣(1)解不等式f(x)＞2.(2)求函数y=f(x)的最小值.
- 不等式的解集是
- （选做题）已知函数f（x）=|x+1|，（1）解不等式f（x）≥2x+1；（2）∃x∈R，使不等式f（x-2）-f（x+6）＜m成立，求m的取值范围．
- 坐标系与参数方程：已知极点与原点重合，极轴与x轴的正半轴重合．若曲线c1的极坐标方程为：5p2-3p2cos2θ-8=0，直线ɛ的参数方...
- ．已知圆C与直线的极坐标方程分别为，求点C到直线的距离是（ ）A．4B．C．D．