本试题 “设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )A.[-12,12]B.[-2,2]C.[-1,1]D.[-4,4]” 主要考查您对直线的倾斜角与斜率
直线的图像特征与倾斜角、斜率的关系
抛物线的性质(顶点、范围、对称性、离心率)
直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线的倾斜角与斜率
- 直线的图像特征与倾斜角、斜率的关系
- 抛物线的性质(顶点、范围、对称性、离心率)
- 直线与抛物线的应用
直线的倾斜角的定义:
x轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。因此,倾斜角的取值范围是0°≤α<180°。
直线的斜率的定义:
倾斜角不是90°的直线,它的倾斜角的正切值叫做这条直线的斜率。直线的斜率常用k表示。即k=tanα。斜率反映直线与x轴的倾斜程度。
直线斜率的性质:
当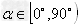 时,k≥0;当
时,k≥0;当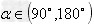 时,k<0;当
时,k<0;当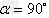 时,k不存在。
时,k不存在。
直线倾斜角的理解:
(1)注意“两个方向”:直线向上的方向、x轴的正方向;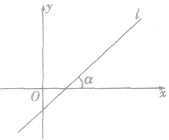
(2)规定当直线和x轴平行或重合时,它的倾斜角为0度。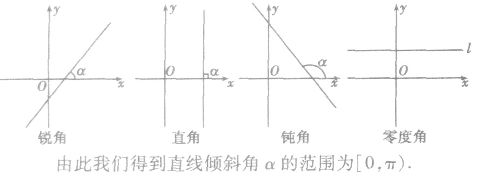
直线倾斜角的意义:
①直线的倾斜角,体现了直线对x轴正向的倾斜程度;
②在平面直角坐标系中,每一条直线都有一个确定的倾斜角;
③倾斜角相同,未必表示同一条直线。
直线斜率的理解:
每条直线都有倾斜角,但每条直线不一定都有斜率, 斜率不存在;当
斜率不存在;当 也逐渐增大;
也逐渐增大; 且逐渐增大。
且逐渐增大。
直线的图像与倾斜角、斜率的关系:
利用直线的倾斜角或者斜率判定函数的图象的形状或者位置。
直线的倾斜角、斜率对直线的图像的影响:
(1)直线在y轴上的截距大于0时:
若倾斜角为锐角,则斜率大于0,这时直线的图像过第一二三象限,并且倾斜角越大斜率就越大,直线相对于x轴的正方向的倾斜程度也就越大;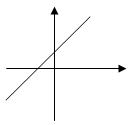
若倾斜角为钝角,则斜率小于0,这时直线的图像过第一二四象限,并且倾斜角越大斜率就越大,直线相对于x轴的正方向的倾斜程度也就越大;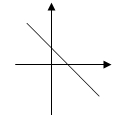
(2)直线在y轴上的截距小于0时:
若倾斜角为锐角,则斜率大于0,这时直线的图像过第一三四象限,并且倾斜角越大斜率就越大,直线相对于x轴的正方向的倾斜程度也就越大;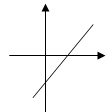
若倾斜角为钝角,则斜率小于0,这时直线的图像过第二三四象限,并且倾斜角越大斜率就越大,直线相对于x轴的正方向的倾斜程度也就越大;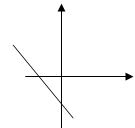
(3)当直线的倾斜角为直角时,斜率不存在,直线的图线与x轴垂直;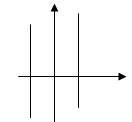
(4)当直线的倾斜角为0度时,斜率为0,直线的图线与x轴平行或重合。
抛物线的性质(见下表):

抛物线的焦点弦的性质:
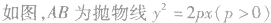
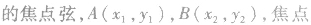

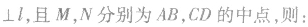

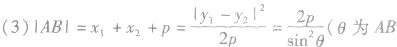

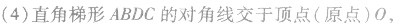


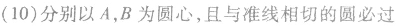
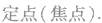
关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部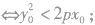 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
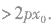
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
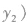 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F,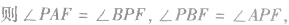 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。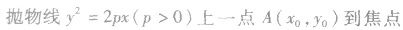
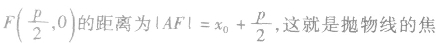
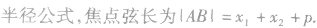
设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
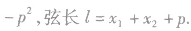
与“设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有...”考查相似的试题有:
- 直线和直线的夹角为( )A.B.C.D.
- 倾斜角为135°,在轴上的截距为的直线方程是( )A.B.C.D.
- 设抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线与抛物线交于A、B两点.(1)若p=2,求线段AF中点M的轨迹方程;(2)若直...
- 设函数f(x)=|x+1|+|2x-1|。(1)画出函数y=f(x)的图象;(2)若对任意x∈(-∞,0],f(x)≤ax+b恒成立,求a-b的最大值。
- 若抛物线y2=8x上一点P到其焦点的距离为10,则点P的坐标为( ) A.(8,8) B.(8,-8) C.(8,±8) D.(-8,±8)
- 抛物线y2=4ax(a<0)的焦点坐标是[ ]A.(a,0) B.(﹣a,0) C.(0,a) D.(0,﹣a)
- 抛物线y=(n2+n)x2-(2n+1)x+1(n∈N*),交x轴于An,Bn两点,则|A1B1|+|A2B2|+|A3B3|+…+|A2008B2008|值为______.
- 已知过抛物线y2=2px(p>0)的焦点F的直线交抛物线于M、N两点,直线OM、ON(O为坐标原点)分别与准线l:x=-p2相交于P、Q两点...
- 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|<1)上一点M的切线l,与曲线C2:y=(|x|<1)也相切于点N,记点M的横坐...
- 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点。(1)求m与a的值;...