本试题 “判断。(对的打“√”,错的打“×”)1.把线段比例尺改写成数字比例尺是。[ ]2.正方体、圆柱、长方体的体积都可以用底面积乘高来计算。[ ]3.在由4张,4张,4张...” 主要考查您对年,月,日
长方体的体积
正方体的体积
正比例的意义,反比例的意义
比例尺
圆柱的体积
可能性,概率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 年,月,日
- 长方体的体积
- 正方体的体积
- 正比例的意义,反比例的意义
- 比例尺
- 圆柱的体积
- 可能性,概率
时间单位:
日(天)、星期、月、年、世纪。
月:
大月(31天):一月、三月、五月、七月、八月、十月、十二月;
小月:四月、六月、九月、十一月;
二月:平年28天,闰年29天。
季度:
一年有四个季度:1月、2月、3月属于第一季度;4月、5月、6月属于第二季度;7月、8月、9月属于第三季度;10月、11月、12月属于第四季度。
年:
闰年:通常公历年是4的倍数的是闰年;公历年份是整百数的,须是400的倍数,闰年有366天。
平年:通常公历年不是4的倍数的是平年;公历年份是整百数的,不是400的倍数的是平年,平年有365天。
时间单位之间的进率:
世纪
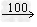 年
年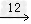 月;1日(天)=24小时;1星期=7天。
月;1日(天)=24小时;1星期=7天。闰年的判断方法:
公历年份可被4整除为闰年,但是正百的年数必须是可以被400整除的才是闰年。
长方体的体积=长×宽×高;V=abh。
长方体的体积=底面积×高;V=sh。
正方体的体积=棱长×棱长×棱长;V=
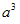 。
。正方体的体积=底面积×高;V=sh。
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: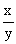 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。
正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(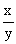 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。
判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
表示图上距离比实地距离缩小的程度,因此也叫缩尺。图上距离和实际距离的比,叫做这幅图的比例尺。
即:图上距离:实际距离=比例尺;
 =比例尺
=比例尺比例尺分类:
比例尺一般分为数值比例尺和线段比例尺:
(1)数值比例尺:例如一幅图的比例尺是1:20000或 。为了方便,通常把比例尺写成前项(或后项)是1的比。
。为了方便,通常把比例尺写成前项(或后项)是1的比。
(2)线段比例尺是在图上附上一条标有数量的线段,用来表示实际相对应的距离。
比例尺表示方法:
用公式表示为:比例尺= 。比例尺通常有三种表示方法。
。比例尺通常有三种表示方法。
①数字式,用数字的比例式或分数式表示比例尺的大小。例如地图上1厘米代表实地距离500千米,可写成:1∶50,000,000或写成:1/50,000,000。
②线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离。
③文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如:图上1厘米相当于地面距离500千米,或五千万分之一。
三种表示方法可以互换。必须化单位。
在绘制地图和其他平面图的时候,需要把实际距离按一定的比缩小(或扩大),再画在图纸上。
这时,就要确定图上距离和相对应的实际距离的比。
比例尺公式:
图上距离=实际距离×比例尺
实际距离=图上距离÷比例尺
比例尺=图上距离÷实际距离
单位换算:
在比例尺计算中要注意单位间的换算:1公里=1千米=1×1000米=1×100000厘米
图上用厘米,实地用千米,厘米换千米,去五个零;
千米换厘米,在千的基础上再加两个零。
计算方法:
①如果将原比例尺放大到n倍;那么原比例×n。
②如果将原比例尺放大n倍;那么原比例×(n+1)。
③如果将原比例尺缩小到1/n;那么原比例×1/n。
④如果将原比例尺缩小1/n;那么原比例×(1-1/n)。
⑤比例尺缩放后,原面积之比会变为缩放倍数的平方。
圆柱的体积公式:
v:体积 h:高 s:底面积 r:底面半径 c:底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高(即v=sh)
(4)底面积=半径×半径×3.14
圆柱的体积=底面积×高即:v=sh=πr2h。
可能性:
是指事物发生的概率,是包含在事物之中并预示着事物发展趋势的量化指标。有些事件的发生是确定的,有些是不确定的。用“可能”、“不可能”“一定”等表达事物发生的情况。
常见方法有:抛骰子、摸球、转盘。
概率:
又称或然率、机会率或机率、可能性,是数学概率论的基本概念,是一个在0到1之间的实数,是对随机事件发生的可能性的度量。
随机事件:
有些事件在一定的条件下可能发生,也可能不发生,结果不确定。例如,购买彩票能否 中奖,开出的列车能否正点到达。明年今天是否下雨等待,我们称之为随机事件。
我们用随机事件的“概率”来表示随机事件发生可能性大小:概率是0到1之间的一个数,概率随机事件发生的可能性大。
在小学阶段我们只计算最简单的一些随机事件的概率,这种计算方法以“等可能性”为基础。在有些情况下,虽然有些事情的结果是不确定的(随机性的),但是由于某种“对称性”,不同的基本结果发生的可能性是相同的,这时,我们说这些基本结果是等可能的,从而确定相关事件的概率。例如:
投一枚均匀硬币,“出现正面”“出现反面”这两种基本结果是等可能的,所以“出现正面”和“出现反面”的概率都是1/2;
投一枚色子(骰子),“出现1点”“出现2点”......“出现6点”这六种基本情况是等可能的,其概率是1/6 。
对于随机事件,我们关心的是事件发生的可能性。
事件发生的可能性大小是可以比较的,所以人们常说一件事情“不可能”""不大可能”“很可能”“非常可能”“绝对可能”......这些说法反应可能性大小的不同程度。
射击时,“射中十环”的可能性比“射中九环”的可能性小;
一分钟投篮,“投中15个”比“投中10个”的可能性小
与“判断。(对的打“√”,错的打“×”)1.把线段比例尺改写成数字比...”考查相似的试题有:
- 一个长方体和一个圆锥体积相等,长方体长8分米,宽6分米,高4分米。圆锥的高比长方体高,求圆锥的底面积。
- 长方体和正方体如果等底等高,那么它们的体积也相等.______.
- 有一个长方体蓄水池,长3米、宽2米、高1.2米.水池里水深0.5米.与水接触的面积是多少平方米?
- 在正方形中,边长和周长______比例面积和边长______比例.
- 在1:300000的地图上,两地相距4厘米,两地的实际距离是______.
- 一个圆柱体的底面半径是4厘米,侧面积是125.6平方厘米,高是______.
- 一个圆柱形水桶,从里面量得底面直径是40厘米,高是40厘米。这个水桶的容积是多少升?
- 在一个底面直径i米,深1.j米的圆柱形水池的内壁和内底面贴上瓷砖,贴瓷砖的面积是多少平方米?这个水池最多可以储水多少立方米?
- 等底等高的圆柱和圆锥的体积相差6dm3,圆锥的体积是______dm3,圆柱的体积是______dm3.
- 转动转盘.指针停在______的可能性最大.指针停在______的可能性最小.