本试题 “已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于______,球的表面积等于______.” 主要考查您对正弦定理
球面距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 球面距离
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即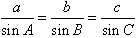 =2R。
=2R。
有以下一些变式:
(1)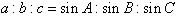 ;
;
(2)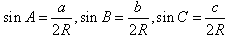 ;
;
(3)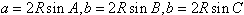 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 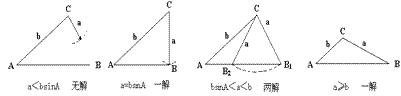
也可根据a,b的关系及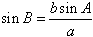 与1的大小关系来确定。
与1的大小关系来确定。
球面距离的概念:
球面上经过两点的大圆在这两点间的一段劣弧的长度,叫做这两点的球面距离。
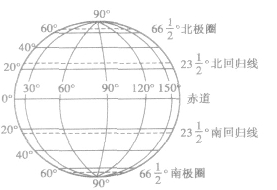
地球上的经纬线:
①当把地球看作一个球时,经线是指球面上从北极到南极的半个大圆.纬线是指垂直于地轴的一组平行平面所截得的圆,纬线除了赤道是大圆外,其余都是小圆.如图所示.
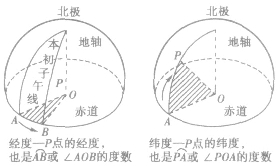
②某点的经度是经过这点的经线与地轴确定的半平面和本初子午线(00经线)与地轴确定的半平面所成的二面角度数.此角实则为二面角,某点的纬度是经过这点的球半径与赤道面所成角的度数,此角实则为线面角.下面用图标注.
对球面距离的理解:
(1)球面上的两点间的球面距离,必须是在球面过此两点的大圆中求此两点所对应的劣弧的长度,不能在过此两点的球的小圆中求.
(2)由于球是旋转体,而旋转体又是轴对称的几何体,因此在解题时,常利用球的轴截面图形来研究问题,从而将空间问题转化为平面问题.
(3)熟练掌握球的截面中大圆的半径,截面圆半径以及球心到截面圆圆心的距离的关系是解决有关球的问题的关键.
发现相似题
与“已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半...”考查相似的试题有:
- 已知为的三个内角的对边,向量,,若,且,则角
- △ABC的三个内角A、B、C的对边分别是a、b、c,如果a2=b(b+c),求证:A=2B.
- 在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
- 在△ABC中,分别为角A、B、C的对边,=3,△ABC的面积为6,,D为△ABC内任一点,点D到三边距离之和为。(1)求:角A的正弦值;(2)求...
- 在△ABC中,a,b,c分别是角A,B,C的对边,且cosBcosC=-b2a+c,则角B的大小为______.
- 在△ABC中,已知b=2,a=2,如果三角形有解,则∠A的取值范围是( )
- 已知△ABC中,AC=1,∠ABC=2π3,∠BAC=x,记f(x)=AB•BC.(1)求f(x)解析式及定义域;(2)设g(x)=6m•f(x)+1,x∈(0,π3),...
- 如图,在某港口A处获悉,其正东方向20海里B处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°据港口10海里的C处,救援...
- 在中,内角A、B、C的对边长分别为、、,已知,且 则b=____________.
- 在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,。(Ⅰ)若△ABC的面积等于,求a,b;(Ⅱ)若,求△ABC的面积.