本试题 “设某物体一天中的温度T是时间的函数:T(t)=at3+bt2+ct+d(a≠0),其中温度的单位是℃,时间单位是小时,t=0表示12:00,取正值表示12:00以后.若测得该物体...” 主要考查您对指数函数模型的应用
对数函数模型的应用
函数解析式的求解及其常用方法
定积分的概念及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数函数模型的应用
- 对数函数模型的应用
- 函数解析式的求解及其常用方法
- 定积分的概念及几何意义
恰当选择自变量将问题的目标表示成自变量的函数f(x)=a·bx+c(a、b、c为常数,a≠0,b>0,b≠1)的形式,进而结合指数函数的性质解决问题。
指数型复合函数的性质的应用:
(1)与指数函数有关的复合函数基本上有两类:![]() ;②
;②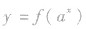 .无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
.无论是哪一类,要搞清楚复合过程,才能确定复合函数的值域和单调区间,具体问题中,a的取值不定时,要对a进行分类讨论.
(2)对于形如![]() 一类的指数型复合函数,有以下结论:
一类的指数型复合函数,有以下结论:
①函数 的定义域与f(x)的定义域相同;
的定义域与f(x)的定义域相同;
②先确定函数f(x)的值域,再根据指数函数的值域、单调性,确定函数 的值域;
的值域;
③当a>l时,函数 与函数f(x)的单调性相同;当O<a<l时,函数
与函数f(x)的单调性相同;当O<a<l时,函数 与函数f(x)的单调性相反.
与函数f(x)的单调性相反.
对数函数模型的定义:
恰当选择自变量将问题的目标表示成自变量的函数f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)的形式,进而结合对数函数的性质解决问题。
对数函数模型解析式:
f(x)=mlogax+n(m、n、a为常数,m≠0,a>0,a≠1)
用函数模型解函数应用题的步骤:
1.审题:弄清题意,分清条件和结论,确定数量关系,初步选择数学模型;
2.建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;
3.求模:求解数学模型,得出数学结论;
4.还原:将数学问题还原为实际问题的意义。
函数解析式的常用求解方法:
(1)待定系数法:(已知函数类型如:一次、二次函数、反比例函数等):若已知f(x)的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得f(x)的表达式。待定系数法是一种重要的数学方法,它只适用于已知所求函数的类型求其解析式。
(2)换元法(注意新元的取值范围):已知f(g(x))的表达式,欲求f(x),我们常设t=g(x),从而求得 ,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
(3)配凑法(整体代换法):若已知f(g(x))的表达式,欲求f(x)的表达式,用换元法有困难时,(如g(x)不存在反函数)可把g(x)看成一个整体,把右边变为由g(x)组成的式子,再换元求出f(x)的式子。
(4)消元法(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等):若已知以函数为元的方程形式,若能设法构造另一个方程,组成方程组,再解这个方程组,求出函数元,称这个方法为消元法。
(5)赋值法(特殊值代入法):在求某些函数的表达式或求某些函数值时,有时把已知条件中的某些变量赋值,使问题简单明了,从而易于求出函数的表达式。
定积分的定义:
设函数f(x)在[a,b]上有界(通常指有最大值和最小值),在a与b之间任意插入n-1个分点,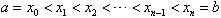 ,将区间[a,b]分成n个小区间
,将区间[a,b]分成n个小区间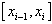 (i=1,2,…,n),记每个小区间的长度为
(i=1,2,…,n),记每个小区间的长度为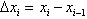 (i=1,2,…,n),在
(i=1,2,…,n),在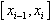 上任取一点ξi,作函数值f(ξi)与小区间长度
上任取一点ξi,作函数值f(ξi)与小区间长度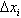 的乘积f(ξi)
的乘积f(ξi)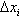 (i=1,2,…,n),并求和
(i=1,2,…,n),并求和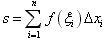 ,记λ=max{△xi;i=1,2,…,n },如果当λ→0时,和s总是趋向于一个定值,则该定值便称为函数f(x)在[a,b]上的定积分,记为
,记λ=max{△xi;i=1,2,…,n },如果当λ→0时,和s总是趋向于一个定值,则该定值便称为函数f(x)在[a,b]上的定积分,记为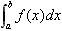 ,即
,即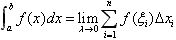 ,其中,
,其中, 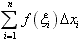 称为函数f(x)在区间[a,b]的积分和。
称为函数f(x)在区间[a,b]的积分和。
定积分的几何意义:
定积分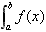 在几何上,
在几何上,
当f(x)≥0时,表示由曲线y=f(x)、直线x=a、直线x=b与x轴所围成的曲边梯形的面积;
当f(x)≤0时,表示由曲线y=f(x)、直线x=a、直线x=b与x轴所围成的曲边梯形的面积的负值;
一般情况下,表示介于曲线y=f(x)、两条直线x=a、x=b与x轴之间的个部分面积的代数和。
定积分的性质:
(1)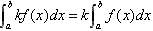 (k为常数);
(k为常数);
(2)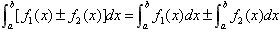 ;
;
(3)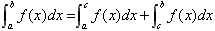 (其中a<c<b)。
(其中a<c<b)。
定积分特别提醒:
①定积分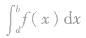 不是一个表达式,而是一个常数,它只与被积函数及积分区间有关,而与积分变量的记法无关,例如:
不是一个表达式,而是一个常数,它只与被积函数及积分区间有关,而与积分变量的记法无关,例如: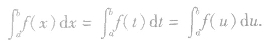
②定义中区间的分法和ξ的取法是任意的,
与“设某物体一天中的温度T是时间的函数:T(t)=at3+bt2+ct+d(a...”考查相似的试题有:
- 美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产...
- 已知n∈{-2,-1,0,1,2,3},若(-12)n>(-15)n,则n=______.
- 设a=0.33,b=30.3,c=log30.3,则a,b,c的大小关系为______.
- 函数f(x)=a2x-ax+b x∈[-1,2],若f (0)=1,f (1)=34,求(1)f (x)的解析式(2)f (x)的值域(3)f (x)的单调区间.
- 不等式3x>127的解集为______.
- (12分)某单位欲用木料制作如下图所示的框架,框架的下部是边长分别为(单位为:)的矩形,上部是等腰直角三角形,要求框架...
- 已知函数f(x)=xm-4x,且f(4)=3(1)求m的值;(2)证明f(x)的奇偶性;(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
- 某乡镇所属A村、B村、C村位于一个边长为a公里的正三角形的三顶点上,乡镇在对外经济改革开放政策中已获得一外资项目,准备在...
- 已知曲线y=xlnx(x>)在点(t,tlnt)处的切线l交x轴于点A,交y轴于点B,△AOB(O为坐标原点)的面积为S,(Ⅰ)试写出S关于t...
- 由抛物线y2=2x与直线y=x-4所围成的图形的面积是( )A.18B.383C.163D.16