本试题 “已知平面上向量,则下列关系式正确的是( )A.B.C.D.” 主要考查您对向量的概念及几何表示
向量数乘运算及几何意义
向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量的概念及几何表示
- 向量数乘运算及几何意义
- 向量数量积的含义及几何意义
向量的概念:
在数学当中,我们把这种既有大小又有方向的量统称为向量。
几何表示:


向量的数乘的定义:
我们规定实数λ与向量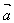 的积是一个向量,记作λ
的积是一个向量,记作λ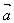 ;
;
向量的数乘的长度和方向规定如下:
(1)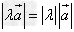 ;
;
(2)当λ>0时,λ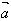 的方向与
的方向与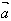 的方向相同;当λ<0时,λ
的方向相同;当λ<0时,λ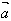 的方向与
的方向与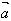 的方向相反;当λ=0时,
的方向相反;当λ=0时,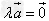 ;注意:λ
;注意:λ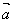 ≠0
≠0
数乘运算的坐标表示:
设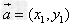 ,则
,则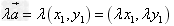 。
。
实数与向量积的运算律:
(1)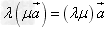 ;
;
(2)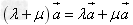 ;
;
(3)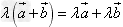 。
。
向量数乘运算的理解:
①向量数乘运算结果仍然是向量.
②实数与向量的积的特殊情况: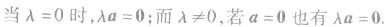
③实数与向量可以求积,但是不能进行加减运算,比如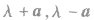 无意义。
无意义。
④由向量数乘的概念可知其几何意义,可以把向量a的长度扩大(当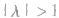 时),也可以缩小(当
时),也可以缩小(当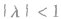 时),同时,我们可以不改变向量a的方向
时),同时,我们可以不改变向量a的方向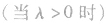 ,也可以改变向量a的方向(当λ<0时)。
,也可以改变向量a的方向(当λ<0时)。
两个向量的夹角的定义:
对于非零向量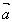 ,
,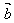 ,作
,作 称为向量
称为向量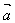 ,
,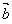 的夹角,当
的夹角,当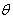 =0时,
=0时,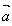 ,
,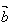 同向,当
同向,当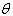 =π时,
=π时,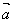 ,
,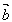 反向,
反向,
当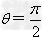 时,
时,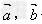 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积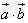 等于
等于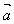 的模
的模 与
与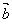 在
在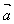 上的投影
上的投影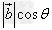 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知平面上向量,则下列关系式正确的是( )A.B.C.D.”考查相似的试题有:
- 已知向量a=(,1),b=(0,-1),c=(k,)。若a-2b与c共线,则k=___________________。
- 设不共线,则下列四组向量中不能作为基底的是( )A.与B.与C.与D.和
- 设,,,是平面直角坐标系中两两不同的四点,若,,且,则称,调和分割,,已知点C(c,0),D(d,0) (c,d∈R)调和分割点A(0,0),...
- 化简( ).A.B.C. D.
- 下列式子正确的是( )A.B.C.≤D.
- 已知正方形ABCD的边长为1,则等于( )A.1B.3C.D.
- 已知A(3,),O为原点,点P(x,y)的坐标满足,则取最大值时点P的坐标是_____
- (本小题满分12分)已知向量与共线,且有函数(Ⅰ)求函数的周期与最大值;(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有,...
- 已知向量a,b,c满足a+b+c=0,且a与c的夹角为60°,|b|=3|a|,则tan<a,b≥( )A.3B.33C.-33D.-3
- =(2,1),=(3,4),则向量在向量方向上的投影为[ ]A.B.C.2D.10