本试题 “设f(x)=Asin(πx2+α)(A≠0),若f(2006)=A,则f(2007)=______.” 主要考查您对三角函数的诱导公式
函数y=Asin(wx+φ)的图象与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角函数的诱导公式
- 函数y=Asin(wx+φ)的图象与性质
诱导公式:
公式一
公式二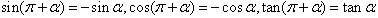
公式三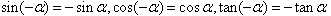
公式四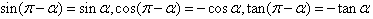
公式五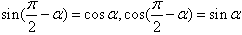
公式六
规律:奇变偶不变,符号看象限。即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。形如2k×90°±α,则函数名称不变。
诱导公式口诀“奇变偶不变,符号看象限”意义:
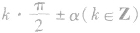 的三角函数值.
的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;
(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。
记忆方法一:奇变偶不变,符号看象限:
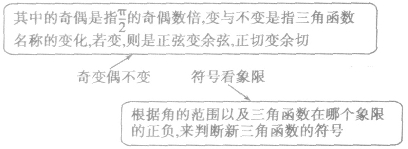
记忆方法二:无论α是多大的角,都将α看成锐角.
以诱导公式二为例:


若将α看成锐角(终边在第一象限),则π十α是第三象限的角(终边在第三象限),正弦函数的函数值在第三象限是负值,余弦函数的函数值在第三象限是负值,正切函数的函数值在第三象限是正值.这样,就得到了诱导公式二.
以诱导公式四为例:

若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负值.这样,就得到了诱导公式四.
以诱导公式四为例:

若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负值.这样,就得到了诱导公式四.
诱导公式的应用:
运用诱导公式转化三角函数的一般步骤:
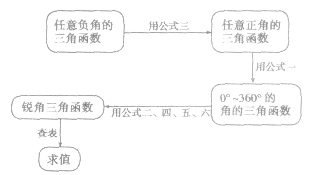
特别提醒:三角函数化简与求值时需要的知识储备:①熟记特殊角的三角函数值;②注意诱导公式的灵活运用;③三角函数化简的要求是项数要最少,次数要最低,函数名最少,分母能最简,易求值最好。

特别提醒:三角函数化简与求值时需要的知识储备:①熟记特殊角的三角函数值;②注意诱导公式的灵活运用;③三角函数化简的要求是项数要最少,次数要最低,函数名最少,分母能最简,易求值最好。
函数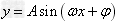 的图象:
的图象:
1、振幅、周期、频率、相位、初相:函数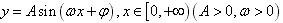 ,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=
,表示一个振动量时,A表示这个振动的振幅,往返一次所需的时间T=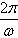 ,称为这个振动的周期,
,称为这个振动的周期,
单位时间内往返振动的次数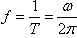 称为振动的频率,
称为振动的频率,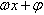 称为相位,x=0时的相位叫初相。
称为相位,x=0时的相位叫初相。
2、用“五点法”作函数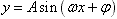 的简图主要通过变量代换,设X=
的简图主要通过变量代换,设X=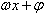 由X取0,
由X取0,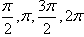 来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
来找出相应的x的值,通过列表,计算得出五点的坐标,描点后得出图象。
3、函数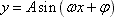 +K的图象与y=sinx的图象的关系:
+K的图象与y=sinx的图象的关系:
把y=sinx的图象纵坐标不变,横坐标向左(φ>0)或向右(φ<0), y=sin(x+φ)
y=sin(x+φ)
把y=sin(x+φ)的图象纵坐标不变,横坐标变为原来的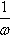 ,
, y=sin(ωx+φ)
y=sin(ωx+φ)
把y=sin(ωx+φ)的图象横坐标不变,纵坐标变为原来的A倍, y=Asin(x+φ)
y=Asin(x+φ)
把y=Asin(x+φ)的图象横坐标不变,纵坐标向上(k>0)或向下(k<0), y=Asin(x+φ)+K;
y=Asin(x+φ)+K;
若由y=sin(ωx)得到y=sin(ωx+φ)的图象,则向左或向右平移 个单位。
个单位。
函数y=Asin(x+φ)的性质:
1、y=Asin(x+φ)的周期为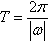 ;
;
2、y=Asin(x+φ)的的对称轴方程是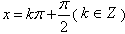 ,对称中心(kπ,0)。
,对称中心(kπ,0)。
发现相似题
与“设f(x)=Asin(πx2+α)(A≠0),若f(2006)=A,则f(2007)=___...”考查相似的试题有:
- 已知是锐角,,则A.B.7C.D.
- 已知,,则等于( )A.B.C.D.
- 若,则的值为( )A. B. C. D.
- 已知函数f(x)=sin(x+7π4)+cos(x-3π4),x∈R(1)求函数图象的对称中心(2)已知cos(β-α)=45,cos(β+α)=-45,0<α<β≤π2...
- 已知sinα=32,则 sin(π-α)=( )A.32B.-32C.12D.-12
- 设函数,(Ⅰ)求f(x)的最小正周期;(Ⅱ)若函数y=g(x)与y=f(x)的图像关于直线x=1对称,求当x∈[0,]时,y=g(x)的最大值。
- 在△ABC中,∠A、∠B、∠C所对的边分别为a,b,c,且a,b,c依次成等比数列,求的取值范围.
- 函数y=cos ()()为奇函数,该函数的部分图像如图所示,A、B分别为最高点与最低点,且|AB|=2,则该函数图象的一条对称轴为[...
- 函数f(x)=sin2x-cos2x的最小正周期是A.B.πC.2πD.4π
- 函数f(x)=2sin(-x)(x∈(0,π))的单调增区间为( )。