本试题 “设函数f(x)=x33+a2x2+bx+c(a,b,c∈R),函数f(x)的导数记为f'(x).(1)若a=f'(2),b=f'(1),c=f'(0),求a、b、c的值;(2)在(1)的条件下,记F...” 主要考查您对综合法与分析法证明不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 综合法与分析法证明不等式
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用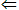 简化叙述。即B
简化叙述。即B C
C D
D …
… A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B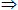 C
C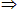 D
D …
…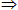 A。
A。
用综合法分析法证明不等式常用到的结论:

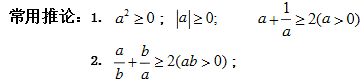
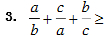 3,
3,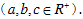
发现相似题
与“设函数f(x)=x33+a2x2+bx+c(a,b,c∈R),函数f(x)的导数记...”考查相似的试题有:
- 设x,y∈R*且x+y=1,求证:。
- 已知f(x)是R上的增函数,a,b∈R.证明下面两个命题:(1)若a+b>0,则f(a)+f(b)>f(-a)+f(-b);(2)若f(a)+f(...
- 已知,.(n∈N*,a为常数)(1)若,求证:数列是等比数列;(2)在(1)条件下,求证:;(3)若a=0,试问代数式的值在哪两...
- 设{an}是等差数列,an>0,公差d≠0,求证:an+1+an+4<an+2+an+3.
- 数学中的综合法是( ) A.由结果追溯到产生原因的思维方法 B.由原因推导到结果的思维方法 C.由反例说明结果不成立的思维方...
- 设x>0,y>0且x≠y,求证
- 某同学在一次研究性学习中发现,以下四个不等式都是正确的:①(12+42)(92+52)≥(1×9+4×5)2;②[(-6)2)+82]×(22+122)≥...
- 对于命题P:存在一个常数M,使得不等式对任意正数a,b恒成立,(1)试猜想常数M的值,并予以证明;(2)类比命题P,某同学猜...
- 设,求证:。
- 已知:a,b,c,d∈R,求证:(ac+bd)2≤(a2+b2)(c2+d2).