本试题 “已知等比数列{an}满足a1=3,且4a1,2a2,a3成等差数列,则此数列的公比等于A.1B.-1C.-2D.2” 主要考查您对等差中项
等比数列的定义及性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差中项
- 等比数列的定义及性质
等差中项:
若a,A,b成等差数列,那么A叫做a与b的等差中项,且2A=a+b,即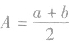 ,反之,若
,反之,若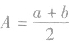 ,则a,A,b成等差数列。
,则a,A,b成等差数列。
等差数列中相邻三项之间存在如下关系:
(1)
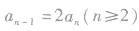 反之,若数列中相邻三项之间存在如下关系:
反之,若数列中相邻三项之间存在如下关系: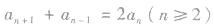 则该数列是等差数列,
则该数列是等差数列,
(2) 若a,A,b成等差数列,那么 2A=a+b,A-a =b -A,a-A =A -b都是等价的.
2A=a+b,A-a =b -A,a-A =A -b都是等价的.
等比数列的定义:
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做公比,公比通常用字母q表示(q≠0)。
等比数列的性质:
在等比数列{an}中,有
(1)若m+n=p+q,m,n,p,q∈N*,则aman=apaq;当m+n=2p时,aman=ap2;
(2)若m,n∈N*,则am=anqm-n;
(3)若公比为q,则{ }是以
}是以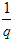 为公比的等比数列;
为公比的等比数列;
(4)下标成等差数列的项构成等比数列;
(5)
1)若a1>0,q>1,则{an}为递增数列;
2)a1<0,q>1, 则{an}为递减数列;
3)a1>0,0<q<1,则{an}为递减数列;
4)a1<0, 0<q<1, 则{an}为递增数列;
5)q<0,则{an}为摆动数列;若q=1,则{an}为常数列。
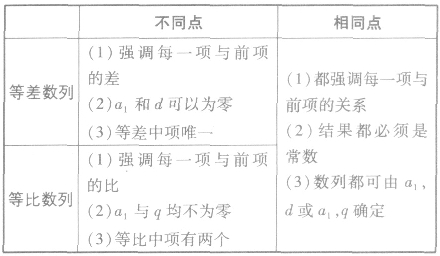
等差数列和等比数列的比较:
如何证明一个数列是等比数列:
证明一个数列是等比数列,只需证明 是一个与n无关的常数即可(或an2=an-1an+1)。
是一个与n无关的常数即可(或an2=an-1an+1)。
发现相似题
与“已知等比数列{an}满足a1=3,且4a1,2a2,a3成等差数列,则此...”考查相似的试题有:
- 已知数列是正项等比数列,若,,则数列的前n项和的最大值为 .
- 在等比数列an,a3=12,S3=32,则首项a1=( )A.14B.-1C.12或2D.-22
- 若等比数列的首项为,且,则公比等于 。
- 观察下列三角形数表1 -----------第一行2 2 -----------第二行3 4 3 -----------第三行4 7 7 4 -----------第四行5 11 14 11 ...
- 设数列的前n项和为,且().(1)求,,,的值;(2)猜想的表达式,并加以证明。
- 已知数列{}的前n项和 (Ⅰ) 求数列{}的通项公式;(Ⅱ) 设,求数列的前.
- 如图3所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第行有个数且两端的数均为,每个数是它下一行左右...
- 若是与的等比中项,则的最小值是 .
- 已知等比数列中,有,数列是等差数列,且,则=A.2B.4C.8D.16
- 对于各项均为整数的数列,如果为完全平方数,则称数列具有“性质”,不论数列是否具有“性质”,如果存在与不是同一数列的,且同...