本试题 “已知:a=110-3,b=110+3,则a2+b2-2的值等于( )A.5B.6C.7D.8” 主要考查您对二次根式的定义
最简二次根式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次根式的定义
- 最简二次根式
二次根式:
我们把形如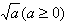 叫做二次根式。
叫做二次根式。
二次根式必须满足:
含有二次根号“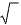 ”;
”;
被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
(1)a≥0 ; ≥0 (双重非负性 );
≥0 (双重非负性 );
(2) ;
;
(3)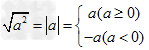
0(a=0);
(4)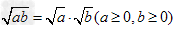 ;
;
(5) 。
。
我们把形如
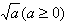 叫做二次根式。
叫做二次根式。二次根式必须满足:
含有二次根号“
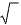 ”;
”;被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式
 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。 二次根式性质:
(1)a≥0 ;
 ≥0 (双重非负性 );
≥0 (双重非负性 );(2)
 ;
;(3)
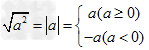
0(a=0);
(4)
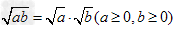 ;
;(5)
 。
。二次根式判定:
①二次根式必须有二次根号,如 ,
,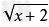 等;
等;
②二次根式 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式;
③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式 是一个非负数;
是一个非负数;
⑤二次根式与算术平方根有着内在的联系, (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。
二次根式的应用:
主要体现在两个方面:
(1)利用从特殊到一般,在由一般到特殊的重要思想方法,解决一些规律探索性问题;
(2)利用二次根式解决长度、高度计算问题,根据已知量,求出一些长度或高度,或设计省料的方案,以及图形的拼接、分割问题。这个过程需要用到二次根式的计算,其实就是化简求值。
最简二次根式定义:
被开方数中不含字母,并且被开方数中所有因式的幂的指数都小于2,这样的二次根式称为最简二次根式。
有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,则说这两个代数式互为有理化因式。
最简二次根式同时满足下列三个条件:
(1)被开方数的因数是整数,因式是整式;
(2)被开方数中不含有能开的尽的因式;
(3)被开方数不含分母。
最简二次根式判定:
①在二次根式的被开方数中,只要含有分数或小数就不是最简二次根式;
②在二次根式的被开方数中的每一个因式(或因数),如果幂的指数等于或大于2,也不是最简二次根式。
化二次根式为最简二次根式的方法和步骤:
①如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简。
②如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来。
发现相似题
与“已知:a=110-3,b=110+3,则a2+b2-2的值等于( )A.5B.6C....”考查相似的试题有:
- 若,化简=( ▼ )A.B.C.D.
- 设点P的坐标是(1+-a,-2+a),则点P在( )A.第一象限B.第二象限C.第三象限D.第四象限
- 比较大小:35______26.
- 当 时,在实数范围内有意义
- 若,则x的取值范围是( )。
- 在函数中,自变量x的取值范围是[ ]A.B.x>-1且C.x≥-1且D.x>-1
- 实数a在数轴上的位置如图所示,则(3-a)2-(a-11)2化简后为______.
- 计算:20110-+︱-3︱.
- (体验探究题)阅读下面的文字后,回答问题:题目:已知a+1-2a+a2,其中a=9,先化简式子,再求值.下面为小明和小芳的解答....
- 方程(2+1)x=2+2的解是______.