本试题 “如图,在长方体ABCDA1B1C1D1中,已知AB=4,AD=3,AA1=2,E,F分别是棱AB,BC上的点,且EB=FB=1. (1)求异面直线EC1与FD1所成角的余弦值;(2)试在面A1B1C...” 主要考查您对空间向量的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 空间向量的定义
空间向量的定义:
在空间中,我们把具有大小和方向的量叫做向量。
空间向量的坐标表示:
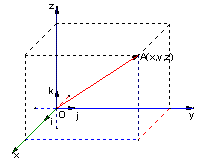
如图给定空间直角坐标系和向量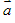 ,设
,设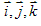 为坐标向量,则存在唯一的有序实数组
为坐标向量,则存在唯一的有序实数组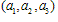 ,使
,使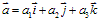 ,有序实数组
,有序实数组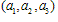 叫作向量
叫作向量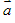 在空间直角坐标系
在空间直角坐标系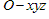 中的坐标,记作
中的坐标,记作 。
。
空间向量的理解:
(1)向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量;
(2)空间的两个向量可用同一平面内的两条有向线段来表示。
发现相似题
与“如图,在长方体ABCDA1B1C1D1中,已知AB=4,AD=3,AA1=2,...”考查相似的试题有:
- 如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则点O到平面ABC1D1的距离为 .
- 已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共面,则实数λ= .
- 如图P为空间中任意一点,动点Q在△ABC所在平面内运动,且,则实数m=( ) A.0 B.2 C.-2 D.1
- 已知向量=(cos120°,sin120°),=(cos30°,sin30°),则△ABC的形状为A.直角三角形B.钝角三角形C.锐角三角形D.等边三角形
- 在空间直角坐标系中,若点A(1,2,﹣1),B(﹣3,﹣1,4).则|AB|= .
- 如图所示,直三棱柱ABCA1B1C1中,D、E分别是AB、BB1的中点,AA1=AC=CB=AB.(1)证明:BC1∥平面A1CD;(2)求二面角DA1CE的正弦...
- 在中,,,,为边上的高,为的中点,若,则的值为. . . .
- 已知,,则下面说法中,正确的个数是 ( )(1)线段AB的中点坐标为;(2)线段AB的长度为;(3)到A,B两点的距离相等的点的坐...
- 已知正四棱锥中,高是4米,底面的边长是6米。(1)求正四棱锥的体积;(2)求正四棱锥的表面积.
- 在如图所示的几何体中,四边形是等腰梯形,∥,,.在梯形中,∥,且,⊥平面.(1)求证:;(2)若二面角为,求的长.