本试题 “若关于x的方程x2-3kx-1=0有实数根,则k的取值范围为( )A.k≥0B.k>0C.k≥-49D.k>-49” 主要考查您对二次根式的定义
一元二次方程根的判别式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次根式的定义
- 一元二次方程根的判别式
二次根式:
我们把形如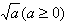 叫做二次根式。
叫做二次根式。
二次根式必须满足:
含有二次根号“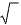 ”;
”;
被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
(1)a≥0 ; ≥0 (双重非负性 );
≥0 (双重非负性 );
(2) ;
;
(3)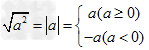
0(a=0);
(4)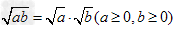 ;
;
(5) 。
。
我们把形如
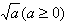 叫做二次根式。
叫做二次根式。二次根式必须满足:
含有二次根号“
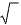 ”;
”;被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式
 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。 二次根式性质:
(1)a≥0 ;
 ≥0 (双重非负性 );
≥0 (双重非负性 );(2)
 ;
;(3)
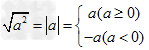
0(a=0);
(4)
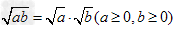 ;
;(5)
 。
。二次根式判定:
①二次根式必须有二次根号,如 ,
,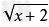 等;
等;
②二次根式 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式;
③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式 是一个非负数;
是一个非负数;
⑤二次根式与算术平方根有着内在的联系, (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。
二次根式的应用:
主要体现在两个方面:
(1)利用从特殊到一般,在由一般到特殊的重要思想方法,解决一些规律探索性问题;
(2)利用二次根式解决长度、高度计算问题,根据已知量,求出一些长度或高度,或设计省料的方案,以及图形的拼接、分割问题。这个过程需要用到二次根式的计算,其实就是化简求值。
根的判别式:
一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac。
定理1 ax2+bx+c=0(a≠0)中,△>0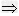 方程有两个不等实数根;
方程有两个不等实数根;
定理2 ax2+bx+c=0(a≠0)中,△=0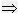 方程有两个相等实数根;
方程有两个相等实数根;
定理3 ax2+bx+c=0(a≠0)中,△<0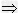 方程没有实数根。
方程没有实数根。
根的判别式逆用(注意:根据课本“反过来也成立”)得到三个定理。
定理4 ax2+bx+c=0(a≠0)中,方程有两个不等实数根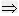 △>0;
△>0;
定理5 ax2+bx+c=0(a≠0)中,方程有两个相等实数根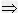 △=0;
△=0;
定理6 ax2+bx+c=0(a≠0)中,方程没有实数根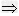 △<0。
△<0。
注意:(1)再次强调:根的判别式是指△=b2-4ac。
(2)使用判别式之前一定要先把方程变化为一般形式,以便正确找出a、b、c的值。
(3)如果说方程,即应当包括有两个不等实根或有两相等实根两种情况,此时b2-4ac≥0切勿丢掉等号。
(4)根的判别式b2-4ac的使用条件,是在一元二次方程中,而非别的方程中,因此,要注意隐含条件a≠0。
根的判别式有以下应用:
①不解一元二次方程,判断根的情况。
②根据方程根的情况,确定待定系数的取值范围。
③证明字母系数方程有实数根或无实数根。
④应用根的判别式判断三角形的形状。
⑤判断当字母的值为何值时,二次三项是完全平方式。
⑥可以判断抛物线与直线有无公共点。
⑦可以判断抛物线与x轴有几个交点。
⑧利用根的判别式解有关抛物线 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。
一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac。
定理1 ax2+bx+c=0(a≠0)中,△>0
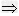 方程有两个不等实数根;
方程有两个不等实数根;定理2 ax2+bx+c=0(a≠0)中,△=0
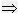 方程有两个相等实数根;
方程有两个相等实数根;定理3 ax2+bx+c=0(a≠0)中,△<0
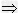 方程没有实数根。
方程没有实数根。根的判别式逆用(注意:根据课本“反过来也成立”)得到三个定理。
定理4 ax2+bx+c=0(a≠0)中,方程有两个不等实数根
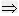 △>0;
△>0;定理5 ax2+bx+c=0(a≠0)中,方程有两个相等实数根
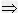 △=0;
△=0;定理6 ax2+bx+c=0(a≠0)中,方程没有实数根
 △<0。
△<0。注意:(1)再次强调:根的判别式是指△=b2-4ac。
(2)使用判别式之前一定要先把方程变化为一般形式,以便正确找出a、b、c的值。
(3)如果说方程,即应当包括有两个不等实根或有两相等实根两种情况,此时b2-4ac≥0切勿丢掉等号。
(4)根的判别式b2-4ac的使用条件,是在一元二次方程中,而非别的方程中,因此,要注意隐含条件a≠0。
根的判别式有以下应用:
①不解一元二次方程,判断根的情况。
②根据方程根的情况,确定待定系数的取值范围。
③证明字母系数方程有实数根或无实数根。
④应用根的判别式判断三角形的形状。
⑤判断当字母的值为何值时,二次三项是完全平方式。
⑥可以判断抛物线与直线有无公共点。
⑦可以判断抛物线与x轴有几个交点。
⑧利用根的判别式解有关抛物线
 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。 发现相似题
与“若关于x的方程x2-3kx-1=0有实数根,则k的取值范围为( )A.k...”考查相似的试题有:
- 下列数中,0.4583,,3.14,,,,0.373373337… 是无理数的有( )A.2个B.3个C.4个D.5个
- 当时,二次根式的值为【 】A.1B.±1C.3D.±3
- 若+(n+1)2=0,则m+n的值为_________.
- 在实数范围内,使式子13-x有意义的x的取值范围是( )A.x=3B.x<3C.x>3D.x≥3
- 中自变量x的取值范围是( )A.B.C.D.
- 要使二次根式,则的取值范围是( )A.B.C.D.
- 函数的自变量x 的取值范围是( )。
- y=x-8+8-x+17,求x+y的算术平方根.
- 二次根式的值是( )A.B.或C.D.
- 已知关于x的一元二次方程x2-2x+k=0.(1)当方程有两个实数根时,求实数k的取值范围;(2)当方程无实数根时,求实数k的取值...