本试题 “已知2a=3b=k(k≠1),且2a+b=ab,则实数k的值为( ) A.6 B.9 C.12 D.18” 主要考查您对对数函数的图象与性质
指数式与对数式的互化
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数函数的图象与性质
- 指数式与对数式的互化
对数函数的图形:
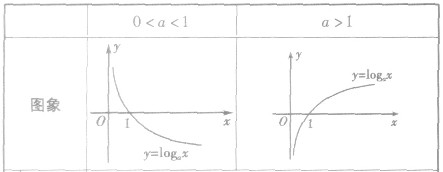
对数函数的图象与性质:
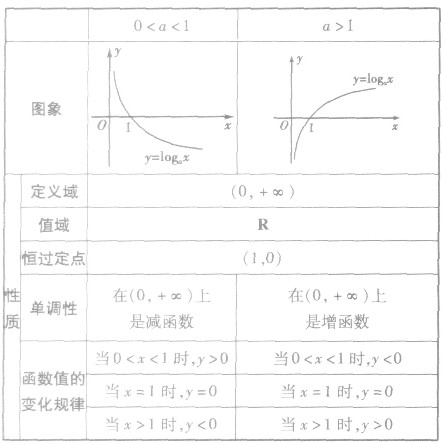
对数函数与指数函数的对比:
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: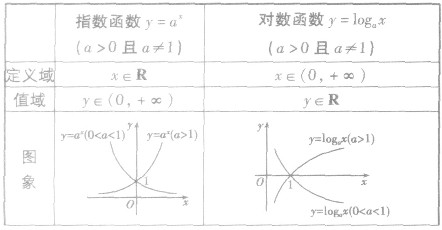
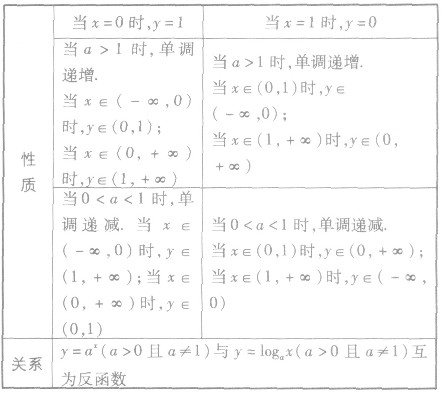
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
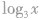 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
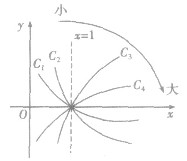
2.类似地,在同一坐标系中分别作出
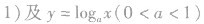 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如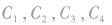 分别对应函数
分别对应函数
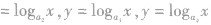 ,则必有
,则必有
指数式与对数式的互化:
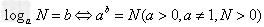 。
。
指数式与对数式的关系:
(1)对数由指数而来。对数式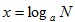 是由指数式
是由指数式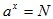 而来的,两式底数相同,对数中的真数N就是指数中的幂的值N,而对数值
而来的,两式底数相同,对数中的真数N就是指数中的幂的值N,而对数值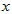 是指数式中的幂指数。
是指数式中的幂指数。
(2)在指数式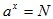 中,若已知a,N的值,求幂指数
中,若已知a,N的值,求幂指数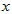 的值,便是对数运算。
的值,便是对数运算。
(3)在互化过程中应注意各自的位置及表示方式。
(4)对数式与指数式的关系及相应各数的名称如下:
| 式子 | 名称 | |||
| a | 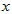 |
N | ||
| 指数式 | 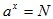 |
底数 | 指数 | 幂 |
| 对数式 | 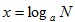 |
底数 | 对数 | 真数 |
与“已知2a=3b=k(k≠1),且2a+b=ab,则实数k的值为( ) A.6 B...”考查相似的试题有:
- 已知函数f(x)=-x+log21-x1+x,则f(12012)+f(-12012)=______.
- 附加题:若函数f(x)=log2(kx2+4kx+3)的定义域为R,求k的取值范围.
- 已知a=5-12,函数f(x)=logax,若正实数m,n满足f(m)>f(n),则m,n的大小关系为______.
- 下列关系式中,成立的是[ ]A.B.C.D.
- 己知f(x)=log2(x+1),当点(x,y)在函数y=f(x)的图象上时,点(-x,-y)在函数y=g(x)的图象上.(1)写出y=g(x)的...
- 若x1满足2x=5-x,x2满足x+log2x=5,则x1+x2等于( )A.2B.3C.4D.5
- 设定义在区间(-b,b)上的函数f(x)=lg1+ax1-2x是奇函数(a,b∈R,且a≠-2),则ab的取值范围是( )A.(1, 2]B.[22, 2]C....
- 已知f(x)=x+log2x,则f(2)+f(4)=[ ]A.11B.10C.9D.8
- 令。如果对,满足为整数,则称k为“好数”,那么区间内所有的“好数”的和S=( )
- 计算:(1)已知a-a-1=1,求a2+a-2-3a4-a-4的值.(2)(lg5)2+lg2•lg50的值.