本试题 “在等差数列{an}中,若a1004+a1005+a1006=3,则该数列的前2009项的和为( )A.3000B.2009C.2008D.2007” 主要考查您对等差数列的前n项和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差数列的前n项和
等差数列的前n项和的公式:
(1)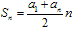 ,(2)
,(2)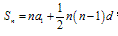 ,(3)
,(3)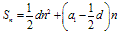 ,(4)
,(4)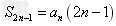
当d≠0时,Sn是关于n的二次函数且常数项为0,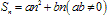
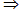 {an}为等差数列,反之不能。
{an}为等差数列,反之不能。
等差数列的前n项和的有关性质:
(1) ,…成等差数列;
,…成等差数列;
(2){an}有2k项时,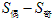 =kd;
=kd;
(3){an}有2k+1项时,S奇=(k+1)ak+1=(k+1)a平, S偶=kak+1=ka平,S奇:S偶=(k+1):k,S奇-S偶=ak+1=a平;
解决等差数列问题常用技巧:
1、等差数列中,已知5个元素:a1,an,n,d, S中的任意3个,便可求出其余2个,即知3求2。
为减少运算量,要注意设元的技巧,如奇数个成等差,可设为…,a-2d,a-d,a,a+d,a+2d,…,偶数个成等差,可设为…,a-3d,a-d,a+d,a+3d,…
2、等差数列{an}中,(1)若ap=q,aq=p,则列方程组可得:d=-1,a1=p+q-1,ap+q=0,S=-(p+q);
(2)当Sp=Sq时(p≠q),数形结合分析可得Sn中最大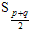 ,Sp+q=0,此时公差d<0。
,Sp+q=0,此时公差d<0。
发现相似题
与“在等差数列{an}中,若a1004+a1005+a1006=3,则该数列的前2009...”考查相似的试题有:
- 在等差数列{an}中,若S9=18,an-4=30,Sn=240.则n等于( ) A.9 B.15 C.9或15 D.24
- 已知等差数列{an}中,a7=3,则数列{an}的前13项之和为[ ]A.B.39C.D.117
- 已知等差数列{an}的前n项和为Sn,且a6=﹣5,S4=﹣62.(1)求{an}通项公式;(2)求数列{|an|}的前n项和Tn.
- 已知{an}是等差数列,a3=4,a6+a9=-10,前n项和为Sn,(1)求通项公式an(2)当n为何值时Sn最大,并求出最大值.
- 如图是一个有n层(n≥2)的六边形点阵它的中心是一个点,算作第一层,第2层每边有2个点,第3层每边有3个点…,第n层每边有n个点,...
- 设Sn是等差数列{an}的前n项和,已知S4=1,S8=4,求a13+a14+a15+a16的值.
- 已知Sn是等差数列{an}(n∈N*)的前n项和,且S5<S6,S6=S7>S8,则下列结论错误的是( ) A.S6和S7均为Sn的最大值. B.a7=0...
- 已知数列{an}的前n项和Sn满足Sn=14(an+1)2,且an>0.(1)求数列{an}的通项公式(2)令bn=20-an,试求数列{bn}的前多少项的...
- 等差数列{an}中,若a4+a6+a8+a10+a12=120,则S15的值为( )A.180B.240C.360D.720
- 已知数列是以d为公差的等差数列,数列是以q为公比的等比数列.(1)若数列的前n项和为Sn,且a1=b1=d=2,S3<a1004+5b2-2012,...