已知数列{an}的前n项和为Sn，a1=3，当n≥2，n∈N*时，Sn-1是an与-3的等差中项，(1)求a2，a3，a4；(2)求数列{a,高中三年级,数学试题,等差中项考点,等比数列的通项公式考点,好技网

解答题
已知数列{a_n}的前n项和为S_n，a₁=3，当n≥2，n∈N*时，S_n-1是a_n与-3的等差中项，
(1)求a₂，a₃，a₄；
(2)求数列{a_n}的通项公式．

本题信息：2011年模拟题数学解答题难度较难来源:张玲玲
本题答案
查看答案

本试题 “已知数列{an}的前n项和为Sn，a1=3，当n≥2，n∈N*时，Sn-1是an与-3的等差中项，(1)求a2，a3，a4；(2)求数列{an}的通项公式．” 主要考查您对
等差中项

等比数列的通项公式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

等差中项
等比数列的通项公式

等差中项:

若a，A，b成等差数列，那么A叫做a与b的等差中项，且2A=a+b,即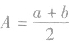，反之，若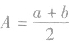，则a，A，b成等差数列。

等差数列中相邻三项之间存在如下关系：

（1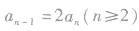）反之，若数列中相邻三项之间存在如下关系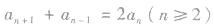：则该数列是等差数列，
（2）若a，A,b成等差数列，那么 2A=a+b，A-a =b -A，a-A =A -b都是等价的．

等比数列的通项公式:

a_n=a₁q^n-1，q≠0，n∈N^*。

等比数列的通项公式的理解：

①在已知a₁和q的前提下，利用通项公式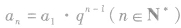可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用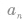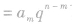可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{a_n}的通项公式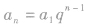，可以改写为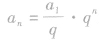．当q>o，且q≠1时，y=q^x是一个指数函数，而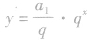是一个不为0的常数与指数函数的积，因此等比数列{a_n}的图象是函数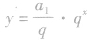的图象上的一群孤立的点；
④通项公式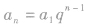亦可用以下方法推导出来：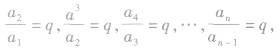

将以上（n一1）个等式相乘，便可得到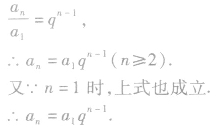

⑤用方程的观点看通项公式．在a_n，q，a₁，n中，知三求一。

发现相似题

与“已知数列{an}的前n项和为Sn，a1=3，当n≥2，n∈N*时，Sn-1是an...”考查相似的试题有：