本试题 “如图,在凸四边形ABCD中,C,D为定点,CD=3,A,B为动点,满足AB=BC=DA=1.(Ⅰ)写出cosC与cosA的关系式;(Ⅱ)设△BCD和△ABD的面积分别为S和T,求S2+T2的最大...” 主要考查您对余弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余弦定理
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: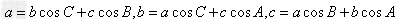
发现相似题
与“如图,在凸四边形ABCD中,C,D为定点,CD=3,A,B为动点,满...”考查相似的试题有:
- (12分)(2011•陕西)叙述并证明余弦定理.
- 在锐角△ABC中,已知a=3,b=2,B=45°求A、C、c及面积S△ABC.
- 已知在△ABC中,三内角A,B,C的对边分别是a,b,c,若,a=,b=1,则c=[ ]A.1B.2C.-1D.
- 在△ABC中,若b2+c2-bc=a2,则A=( )A.150°B.120°C.60°D.30°
- 在△ABC中,内角A、B、C所对的边分别是a、b、c,已知c=2,sinC=32,(1)若sin2B-sinAsinB-2sin2A=0,求a、b的值;(2)若角C...
- 在中,角所对边的长分别为,若,则的最小值为( )A.B.C.D.
- 在f(x)中,a、b、c分别是∠A、∠B、∠C的对边,且b2+c2+3bc=a2,则∠A等于( )A.60°B.30°C.120°D.150°
- 在△ABC中,BC=,AC=3,sinC=2sinA。(1)求AB的值;(2)求sin(2A-)的值。
- 在△ABC中,若,则△ABC的形状为( )。
- 设△ABC是锐角三角形,a,b,c分别是内角A,B,C所对边长,并且sin2A= sin(+B)sin(-B)+sin2B,(Ⅰ)求角A的值;(Ⅱ)若,求b,c(其...