本试题 “函数y=f(x)的导函数y=f′(x)的图象如图所示,则f(x)的解析式可能是( )A.y=axB.y=logaxC.y=xexD.y=xlnx” 主要考查您对函数、映射的概念
导数的概念及其几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数、映射的概念
- 导数的概念及其几何意义
1、映射:
(1)设A,B是两个非空集合,如果按照某一个确定的对应关系f,使对于集合A中的任何一个元素x,在集合B中都有唯一确定的元素y与之对应,
那么,就称对应f:A→B为从集合A到集合B的映射,记作:f:A→B。
(2)像与原像:如果给定一个集合A到集合B的映射,那么,和集合A中的a对应的集合B中的b叫做a的像,a叫做b的原像。
2、函数:
(1)定义(传统):如果在某变化过程中有两个变量x,y并且对于x在某个范围内的每一个确定的值,按照某个对应法则,y都有唯一确定的值和它对应,那么y就是x的函数,x叫做自变量,x的取值范围叫做函数的定义域,和x的值对应的y的值叫做函数值,函数值的集合叫做函数的值域。
(2)函数的集合定义:设A,B都是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任何一个元素x,在集合B中都有唯一确定的数f(x)和它对应,那么就称
f:x→y为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中,x叫做自变量,x的取值范围A叫做函数f(x)的定义域,与x的值相对应的y值叫做函数值,函数值的集合{ f(x)|x∈A}叫做函数f(x)的值域。显然值域是集合B的子集。
3、构成函数的三要素:
定义域,值域,对应法则。
值域可由定义域唯一确定,因此当两个函数的定义域和对应法则相同时,值域一定相同,它们可以视为同一函数。
4、函数的表示方法:
(1)解析法:如果在函数y=f(x)(x∈A)中,f(x)是用代数式(或解析式)来表达的,则这种表示函数的方法叫做解析式法;
(2)列表法:用表格的形式表示两个量之间函数关系的方法,称为列表法;
(3)图象法:就是用函数图象表示两个变量之间的关系。
注意:函数的图象可以是一个点,或一群孤立的点,或直线,或直线的一部分,或若干曲线组成。
映射f:A→B的特征:
(1)存在性:集合A中任一a在集合B中都有像;
(2)惟一性:集合A中的任一a在集合B中的像只有一个;
(3)方向性:从A到B的映射与从B到A的映射一般是不一样的;
(4)集合B中的元素在集合A中不一定有原象,若集合B中元素在集合A中有原像,原像不一定惟一。
(1)函数两种定义的比较:
①相同点:1°实质一致2°定义域,值域意义一致3°对应法则一致
②不同点:1°传统定义从运动变化观点出发,对函数的描述直观,具体生动.
2°近代定义从集合映射观点出发,描述更广泛,更具有一般性.
(2)对函数定义的更深层次的思考:
映射与函数的关系:函数是一种特殊的映射f:A→B,其特殊性表现为集合A,B均为非空的数集. .函数:AB是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与轴的垂线至多有一个公共点,但与轴垂线的公共点可能没有,也可能有任意个。小结:函数概念8个字:非空数集上的映射。
对于映射这个概念,应明确以下几点:
①映射中的两个集合A和B可以是数集,点集或由图形组成的集合以及其它元素的集合.
②映射是有方向的,A到B的映射与B到A的映射往往是不相同的.
③映射要求对集合A中的每一个元素在集合B中都有象,而这个象是唯一确定的.这种集合A中元素的任意性和在集合B中对应的元素的唯一性构成了映射的核心.
④映射允许集合B中的某些元素在集合A中没有原象,也就是由象组成的集合 .
.
⑤映射允许集合A中不同的元素在集合B中有相同的象,即映射只能是“多对一”或“一对一”,不能是“一对多”.
一一映射:设A,B是两个集合,f:A→B是从集合A到集合B的映射,如果在这个映射的作用下,对于集合A中的不同的元素,在集合B中有不同的象,而且B中每一元素都有原象,那么这个映射叫做从A到B上的一一映射. 一一映射既是一对一又是B无余的映射.
在理解映射概念时要注意:⑴A中元素必须都有象且唯一; ⑵B中元素不一定都有原象,但原象不一定唯一。总结:取元任意性,成象唯一性。
对函数概念的理解:
函数三要素
(1)核心——对应法则等式y=f(x)表明,对于定义域中的任意x,在“对应法则f”的作用下,即可得到y.因此,f是使“对应”得以实现的方法和途径.是联系x与y的纽带,从而是函数的核心.对于比较简单的函数,对应法则可以用一个解析式来表示,但在不少较为复杂的问题中,函数的对应法则f也可以采用其他方式(如图表或图象等).
(2)定义域定义域是自变量x的取值范围,它是函数的一个不可缺少的组成部分,定义域不同而解析式相同的函数,应看作是两个不同的函数. 在中学阶段所研究的函数通常都是能够用解析式表示的.如果没有特别说明,函数的定义域就是指能使这个式子有意义的所有实数x的集合.在实际问题中,还必须考虑自变量所代表的具体的量的允许取值范围问题.
(3)值域值域是全体函数值所组成的集合.在一般情况下,一旦定义域和对应法则确定,函数的值域也就随之确定.因此,判断两个函数是否相同,只要看其定义域与对应法则是否完全相同,若相同就是同一个函数,若定义域和对应法则中有一个不同,就不是同一个函数. 同一函数概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。
(4)关于函数符号y=f(x)
1°、y=f(x)即“y是x的函数”这句话的数学表示.仅仅是函数符号,不是表示“y等于f与x的乘积”.f(x)也不一定是解析式.
2°、f(x)与f(a)的区别:f(x)是x的函数,在通常情况下,它是一个变量.f(a)表示自变量x=a时所得的函数值,它是一个常量即是一个数值.f(a)是f(x)的一个当x=a时的特殊值.
3°如果两个函数的定义域和对应法则相同虽然表示自变量的与函数的字母不相同,那么它们仍然是同一个函数,但是如果定义域与对应法则中至少有一个不相同,那么它们就不是同一个函数.
平均变化率:
一般地,对于函数y =f(x),x1,x2是其定义域内不同的两点,那么函数的变化率可用式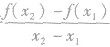 表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用
表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用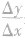 表示,即平均变化率
表示,即平均变化率
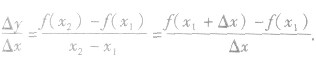
上式中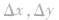 的值可正可负,但
的值可正可负,但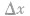 不为0.f(x)为常数函数时,
不为0.f(x)为常数函数时,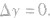
瞬时速度:
如果物体的运动规律是s=s(t),那么物体在时刻t的瞬时速度v就是物体在t到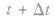 这段时间内,当
这段时间内,当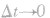 时平均速度的极限,即
时平均速度的极限,即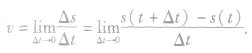
若物体的运动方程为s=f(t),那么物体在任意时刻t的瞬时速度v(t)就是平均速度v(t,d)为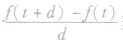 当d趋于0时的极限.
当d趋于0时的极限.
函数y=f(x)在x=x0处的导数的定义:
一般地,函数y=f(x)在x=x0处的瞬时变化率是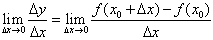 ,我们称它为函数y=f(x)在x=x0处的导数,记作
,我们称它为函数y=f(x)在x=x0处的导数,记作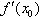 或
或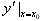 ,即
,即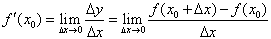 。
。
导函数:
如果函数y =f(x)在开区间(a,6)内的每一点都可导,则称在(a,b)内的值x为自变量,以x处的导数称为f(x为函数值的函数为fx)在(a,b)内的导函数,简称为f(x)在(a,b)内的导数,记作f′(x)或y′.即f′(x)=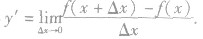
切线及导数的几何意义:
(1)切线:PPn为曲线f(x)的割线,当点Pn(xn,f(xn))(n∈N)沿曲线f(x)趋近于点P(x0,f(x0))时,割线PPn趋近于确定的位置,这个确定的位置的直线PT称为点P处的切线。
(2)导数的几何意义:函数f(x)在x=x0处的导数就是切线PT的斜率k,即k=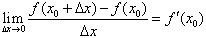 。
。
瞬时速度特别提醒:
①瞬时速度实质是平均速度当 时的极限值.
时的极限值.
②瞬时速度的计算必须先求出平均速度,再对平均速度取极限,
函数y=f(x)在x=x0处的导数特别提醒:
①当 时,比值
时,比值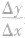 的极限存在,则f(x)在点x0处可导;若
的极限存在,则f(x)在点x0处可导;若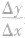 的极限不存在,则f(x)在点x0处不可导或无导数.
的极限不存在,则f(x)在点x0处不可导或无导数.
②自变量的增量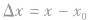 可以为正,也可以为负,还可以时正时负,但
可以为正,也可以为负,还可以时正时负,但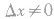 .而函数的增量
.而函数的增量 可正可负,也可以为0.
可正可负,也可以为0.
③在点x=x0处的导数的定义可变形为:

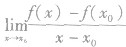
导函数的特点:
①导数的定义可变形为: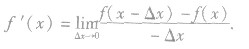
②可导的偶函数其导函数是奇函数,而可导的奇函数的导函数是偶函数,
③可导的周期函数其导函数仍为周期函数,
④并不是所有函数都有导函数.
⑤导函数 与原来的函数f(x)有相同的定义域(a,b),且导函数
与原来的函数f(x)有相同的定义域(a,b),且导函数 在x0处的函数值即为函数f(x)在点x0处的导数值.
在x0处的函数值即为函数f(x)在点x0处的导数值.
⑥区间一般指开区间,因为在其端点处不一定有增量(右端点无增量,左端点无减量).
导数的几何意义(即切线的斜率与方程)特别提醒:
①利用导数求曲线的切线方程.求出y=f(x)在x0处的导数f′(x);利用直线方程的点斜式写出切线方程为y-y0 =f′(x0)(x- x0).
②若函数在x= x0处可导,则图象在(x0,f(x0))处一定有切线,但若函数在x= x0处不可导,则图象在(x0,f(x0))处也可能有切线,即若曲线y =f(x)在点(x0,f(x0))处的导数不存在,但有切线,则切线与x轴垂直.
③注意区分曲线在P点处的切线和曲线过P点的切线,前者P点为切点;后者P点不一定为切点,P点可以是切点也可以不是,一般曲线的切线与曲线可以有两个以上的公共点,
④显然f′(x0)>0,切线与x轴正向的夹角为锐角;f′(x0)<o,切线与x轴正向的夹角为钝角;f(x0) =0,切线与x轴平行;f′(x0)不存在,切线与y轴平行.
与“函数y=f(x)的导函数y=f′(x)的图象如图所示,则f(x)的解...”考查相似的试题有:
- (12分)已知是一次函数,且满足:,求.
- 已知函数f(x)(xR)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )A.B.1C.D.2
- 已知映射,其中集合,若对于,都有使得成立,称该映射为从集合到集合的一个“满射”。则从集合到集合可以建立( )个“满射”。A...
- (本小题满分12分)2010年11月在广州召开亚运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,...
- 对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有...
- 已知点P(-1,1),点Q(2,4)是曲线y=x2上的两点,求与直线PQ平行的曲线y=x2的切线方程。
- 曲线y=x2在(1,1)处的切线方程是( ).
- 一火车锅炉每小时消耗的费用与火车行驶的速度的立方成正比,已知当速度为每小时时,每小时消耗的煤价值元,至于其他费用每小...
- 一质点做直线运动,由始点经过后的距离为,则速度为的时刻是( )A.B.C.与D.与
- 已知函数的图像为曲线C,若曲线C存在与直线垂直的切线,则实数m的取值范围是( )A.B.C.D.