本试题 “如图,已知椭圆的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线交x轴于点K,左顶点为A。(Ⅰ)求证:KF平分∠MKN;(Ⅱ)直线AM、AN分别交准线于点P、...” 主要考查您对椭圆的定义
直线与椭圆方程的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 椭圆的定义
- 直线与椭圆方程的应用
椭圆的第一定义:
平面内与两个定点为F1,F2的距离的和等于常数(大于 )的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。特别地,当常数等于
)的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。特别地,当常数等于 时,轨迹是线段F1F2,当常数小于
时,轨迹是线段F1F2,当常数小于 时,无轨迹。
时,无轨迹。
椭圆的第二定义:
平面内到定点F的距离和到定直线l的距离之比等于常数e(0<e<1)的点的轨迹,叫做椭圆,定点F叫椭圆的焦点,定直线l叫做椭圆的准线,e叫椭圆的离心率。
椭圆的定义应该包含几个要素:
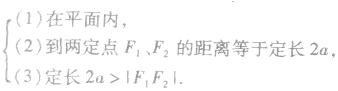
利用椭圆的定义解题:
当题目中出现一点在椭圆上的条件时,注意使用定义

直线与椭圆的方程:
设直线l的方程为:Ax+By+C=0(A、B不同时为零),椭圆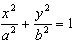 (a>b>0),将直线的方程代入椭圆的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
(a>b>0),将直线的方程代入椭圆的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
椭圆的焦半径、焦点弦和通径:
(1)焦半径公式:
①焦点在x轴上时:|PF1|=a+ex0,|PF2|=a-ex0;
②焦点在y轴上时:|PF1|=a+ey0,|PF2|=a-ey0;
(2)焦点弦:
过椭圆焦点的弦称为椭圆的焦点弦.设过椭圆 的弦为AB,其中A(x1,y1),B(x2,y2),则|AB|=2a+e(x1+x2).由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数.
的弦为AB,其中A(x1,y1),B(x2,y2),则|AB|=2a+e(x1+x2).由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数.
(3)通径:过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆的通径,其长为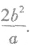
椭圆中焦点三角形的解法:
椭圆上的点与两个焦点F1,F2所构成的三角形,通常称之为焦点三角形,解焦点三角形问题经常使用三角形边角关系定理,解题中,通过变形,使之出现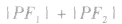 ,这样便于运用椭圆的定义,得到a,c的关系,打开解题思路,整体代换求
,这样便于运用椭圆的定义,得到a,c的关系,打开解题思路,整体代换求 是这类问题中的常用技巧。
是这类问题中的常用技巧。
关于椭圆的几个重要结论:
(1)弦长公式: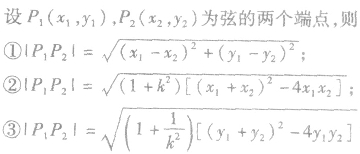
(2)焦点三角形: 上异于长轴端点的点,
上异于长轴端点的点,
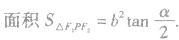
(3)以椭圆的焦半径为直径的圆必与以长轴为直径的圆内切.
(4)椭圆的切线: 处的切线方程为
处的切线方程为
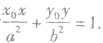
(5)对于椭圆
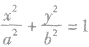 ,我们有
,我们有

发现相似题
与“如图,已知椭圆的右焦点为F,过F的直线(非x轴)交椭圆于M、N...”考查相似的试题有:
- 直线过椭圆的一个焦点,则的值是( )A. B.C. D.
- 如图,点分别是椭圆C:的左、右焦点,过点作轴的垂线,交椭圆的上半部分于点,过点作的垂线交直线于点.(1)如果点的坐标为(4...
- (本小题满分l2分)设椭圆的焦点分别为,直线交轴于点,且.(Ⅰ)试求椭圆的方程;(Ⅱ)过分别作互相垂直的两直线与椭圆分别...
- 已知椭圆的离心率为,其中左焦点①求椭圆的方程②若直线与椭圆交于不同的两点,且线段的中点关于直线的对称点在圆上,求的值
- 设椭圆的焦点在轴上,分别是椭圆的左、右焦点,点是椭圆在第一象限内的点,直线交轴于点,(1)当时,(1)若椭圆的离心率为,...
- 已知F1、F2为椭圆的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|=( )。
- 试确定的取值范围,使得椭圆上有不同两点关于直线对称.
- 椭圆的焦距等于2 ,则的值为 ( )A.5或3B.5C.8D.16
- 已知椭圆的一个顶点为,焦点在轴上,若右焦点到直线的距离为3.(1)求椭圆的标准方程;(2)设直线与椭圆相交于不同的两点、...
- 已知抛物线的焦点与椭圆的一个焦点重合,它们在第一象限内的交点为,且与轴垂直,则椭圆的离心率为( )A.B.C.D.