本试题 “设f(x)在R上可导,其导数为f′(x),给出下列四组条件:①p:f(x)是奇函数,q:f′(x)是偶函数;②p:f(x)是以T为周期的函数,q:f′(x)是以T为周期的函数;③p:f(x...” 主要考查您对充分条件与必要条件
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有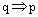 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且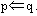 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
发现相似题
与“设f(x)在R上可导,其导数为f′(x),给出下列四组条件:①p:f(x...”考查相似的试题有:
- 已知α、β是不同的两个平面,直线a⊂α,直线b⊂β,命题p:a与b没有公共点;命题q:α∥β,则p是q的 ______条件.
- 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).设p:圆C上存在关于直线l对称的相异两点;q:m=-...
- “x>0”是“x≠0”的[ ]A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
- P:{an}是等比数列(q为{an}的公比);Q:{an}的前n项和为,且P是Q的[ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既...
- 若m、n都是正整数,那么“m、n中至少有一个等于1”是“m+n>mn”的[ ]A.充分而不必要的条件B.必要而不充分的条件C.充要条件D.既不...
- “a>b>0”是“”的[ ]A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
- 已知是直线,是平面,、,则“平面”是“且”的……………………………………………………………………………………………( )A.充要条件.B.充分非必要条件.C.必...
- 下列有关命题的说法正确的有①命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”;②“x=1”是“x2-3x+2=0”的充分不必...
- 已知是的充分条件,而是的必要条件,是的充分条件,是的必要条件。试判断:(1)是的什么条件?(2)是的什么条件?(3)其中...
- 对任意实数a,b,c,给出下列命题:①“”是“”充要条件; ②“是无理数”是“a是无理数”的充要条件;③“”是“”的充分条件;④“”是“”的必...