本试题 “下列语句中错误的是( )A.数轴上的每一个点都有一个实数与它对应B.0.087用科学记数法可表示为8.7×10-2C.据报道:2007年3月18日起,整存整取的三年期定期...” 主要考查您对近似数和有效数字
科学记数法和有效数字
实数的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 近似数和有效数字
- 科学记数法和有效数字
- 实数的定义
一个数与准确数相近(比准确数略多或者略少些),这一个数称之为近似数。
如:我国的人口无法计算准确数目,但是可以说出一个近似数。
比如说我国人口有13亿,13亿就是一个近似数。
有效数字:
是指从该数字左边第一个非0的数字到该数字末尾的数字个数(有点绕口)。例如:
3一共有1个有效数字,0.0003有一个有效数字,0.1500有4个有效数字,1.9×103有两个有效数字(不要被103迷惑,只需要看1.9的有效数字就可以了,10n看作是一个单位)。
精确度:
近似数与准确数的接近程度,可以用精确度表示。
(1)一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位;
(2)规定有效数字的个数,也是对近似数精确程度的一种要求。
有效数字注意:
①近似数的精确度有两种形式:精确到哪一位;保留几个有效数字;
②对于绝对值较大的数取近似值时,结果一般用科学计数法来表示,如:8 90 000(保留三个有效数字)的近似值,得8 903 000≈8.90×106。
③对带有计数单位的近似数,如2.3万,他有两个有效数字:2、3,而不是五个有效数字。
有效数字的舍入规则:
1、当保留n位有效数字,若后面的数字小于第n位单位数字的0.5就舍掉。
2、当保留n位有效数字,若后面的数字大于第n位单位数字的0.5 ,则第位数字进1。
3、当保留n位有效数字,若后面的数字恰为第n位单位数字的0.5 ,则第n位数字若为偶数时就舍掉后面的数字,若第n位数字为奇数加1。
如将下组数据保留三位
45.77=45.8 43.03=43.0
38.25=38.2 47.15=47.2
把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。
有效数字:
从一个数的左边非0数字其,到末尾数字止,所有数字都是这个数的有效数字。
科学记数法的特点:
(1)简单:对于数目很大的数用科学记数法的形式表示起来又科学、又简单。
(2)科学记数法的形式是由两个数的乘积组成的,其中一个因数为a(1≤a<10,a∈N*),另一个因数为10n(n是比原来数A的整数部分少1的正整数)。
(3)用科学记数法表示数时,不改变数的符号,只是改变数的书写形式而已。
速写法:
对于10的指数大于0的情形,数出“除了第一位以外的数位”的个数,即代表0的个数。
如1800000000000,除最高位1外尚有12位,故科学记数法写作1.8×1012或1.8E12。
10的指数小于0的情形,数出“非有效零的总数(第一个非零数字前的所有零的总数)”
如0.00934593,第一位非零数字(有效数字)9前面有3个零,科学记数法写作9.34593×10-3或9.34593E-3。即第一位非零数字前的0的个数为n,就为10-n(n≥0)
科学计数法的基本运算:
数字很大的数,一般我们用科学记数法表示,
例如6230000000000,我们可以用6.23×1012表示,
而它含义从直面上看是将数字6.23中6后面的小数点向右移去12位。
若将6.23×1012写成6.23E12,
即代表将数字6.23中6后面的 小数点向右移去12位,在记数中如
1. 3×104+4×104=7×104可以写成3E4+4E4=7E4
即 aEc+bEc=(a+b)Ec
2. 4×104-7×104=-3×104可以写成4E4-7E4=-3E4
即 aEc-bEc=(a-b)Ec
3. 3000000×600000=1800000000000
3e6×6e5=1.8e12
即 aEM×bEN=abE(M+N)
4. -60000÷3000=-20
-6E4÷3E3=-2E1
即 aEM÷bEN=a/bE(M-N)
5.有关的一些推导
(aEc)2=(aEc)(aEc)=a2E2c
(aEc)3=(aEc)(aEc)(aEc)=a3E3c
(aEc)n=anEnc
a×10lgb=ab
aElgb=ab
实数由有理数和无理数组成,其中无理数就是无限不循环小数,有理数就包括整数和分数。
数学上,实数直观地定义为和数轴上的点一一对应的数。
本来实数仅称作数,后来引入了虚数概念,原本的数称作“实数”——意义是“实在的数”。
实数的定义分析:
1.实数可以分为有理数(如31、
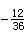 )和无理数(如π、
)和无理数(如π、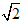 )两类,或代数数和超越数两类,或正数,负数和零三类。
)两类,或代数数和超越数两类,或正数,负数和零三类。2.实数集合通常用字母“R”表示。实数可以用来测量连续的量。
3.理论上,任何实数都可以用无限小数的方式表示,小数点的右边是一个无穷的数列(可以是循环的,也可以是非循环的)。
在实际运用中,实数经常被近似成一个有限小数(保留小数点后n位,n为正整数)。
4.通常把正实数和零合称为分负数,把负实数和零合称为非正数。
5.任何两个实数之间都有无数个有理数和无理数。
实数的性质:
1.基本运算:
实数可实现的基本运算有加、减、乘、除、平方等,对非负数还可以进行开方运算。
实数加、减、乘、除(除数不为零)、平方后结果还是实数。
任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数。
有理数范围内的运算律、运算法则在实数范围内仍适用:
交换律:a+b=b+a , ab=ba
结合律:(a+b)+c=a+(b+c)
分配律:a(b+c)=ab+ac
2.实数的相反数:
实数的相反数的意义和有理数的相反数的意义相同。
实数只有符号不同的两个数,它们的和为零,我们就说其中一个是另一个的相反数。
实数a的相反数是-a,a和-a在数轴上到原点0的距离相等。
3.实数的绝对值:
实数的绝对值的意义和有理数的绝对值的意义相同。一个正实数的绝对值等于它本身;
一个负实数的绝对值等于它的相反数,0的绝对值是0,实数a的绝对值是 :|a|
①a为正数时,|a|=a(不变)
②a为0时, |a|=0
③a为负数时,|a|= a(为a的相反数)
(任何数的绝对值都大于或等于0,因为距离没有负的。)
4实数的倒数:
实数的倒数与有理数的倒数一样,如果a表示一个非零的实数,那么实数a的倒数是:1/a (a≠0)
实数的分类:
(1)按定义分类:
正整数
整数 { 零
负整数
有理数{ }有限小数或无限循环小数
真分数
分数{
实数{ 负分数
正无理数
无理数{ }无限不循环小数
负无理数
(2)按性质分类:
正整数
正有理数{
正实数{ 正分数
正无理数
实数{ 零 负整数
负有理数{
负实数{ 负分数
负无理数
与“下列语句中错误的是( )A.数轴上的每一个点都有一个实数与...”考查相似的试题有:
- 下列数据中是近似数的是[ ]A.七(2)班有54名学生B.足球比赛开始时每方各有11名球员C.杨老师在交通银行存入1000元D.我国...
- 要制造一个容积为2m3的圆柱形容器,且高是底面直径的2倍,求容器的高与底面半径(结果保留3个有效数字).
- 沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( )A.25.3×105亩B.2.53×106亩C.253×1...
- 太阳半径大约是696 000千米,用科学记数法表示为( )米.
- 沈阳市水质监测部门2006年全年共监测水量达48909.6万吨,水质达标率为100%.用科学记数法表示2006全年共监测水量多少万吨(保...
- 写出“一百二十九万”这个数,并且用科学记数法表示:______.
- 冥王星围绕太阳公转的轨道半径长度约为5 900 000 000千米,这个数用科学记数法表示是( )A.5.9×1010千米B.5.9×109千米C.5...
- 1纳米=0.000000001米,一个氢原子的直径是0.12纳米,用科学记数法表示一个氢原子的直径是( )米.A.1.2×10-9B.1.2×10-10C...
- 一张薄的金箔的厚度为0.000000091m,用科学记数法可表示﹙ ﹚m.
- 2009年中央预算用于教育、医疗卫生、社会保障、就业等方面的民生支出达到7285亿元,用科学记数法表示为[ ]A.7285×108元B.72.8...