本试题 “如图,在组合体中,ABCD—A1B1C1D1是一个长方体,P—ABCD是一个四棱锥.AB=2,BC=3,点P平面CC1D1D,且PC=PD=.(1)证明:PD平面PBC;(2)求PA与平面ABCD所成...” 主要考查您对点到直线、平面的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点到直线、平面的距离
点到直线的距离:
由点向直线引垂线,这一点到垂足之间的距离。
点到平面的距离:
由点向平面引垂线,这点到垂足之间的距离,就叫做点到平面的距离。
求点面距离常用的方法:
(1)直接利用定义
①找到(或作出)表示距离的线段;
②抓住线段(所求距离)所在三角形解之.
(2)利用两平面互相垂直的性质如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.
(3)体积法其步骤是:①在平面内选取适当三点和已知点构成三棱锥;②求出此三棱锥的体积V和所取三点构成三角形的面积S;③由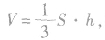 求出
求出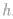 .这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
.这种方法的优点是不必作出垂线即可求点面距离,难点在于如何构造合适的三棱锥以便于计算.
(4)转化法:将点到平面的距离转化为直线与平面的距离来求.
(5)向量法:

发现相似题
与“如图,在组合体中,ABCD—A1B1C1D1是一个长方体,P—ABCD是一个...”考查相似的试题有:
- (本题满分10分) 如图,P—ABCD是正四棱锥,是正方体,其中 (1)求证:;(2)求平面PAD与平面所成的锐二面角的余弦值;
- .在棱长为2的正方体中,动点在内,且到直线的距离之和等于,则的面积最大值是 ( )A.B.1C.2D.4
- 长方体的侧棱,底面的边长,为的中点;(1)求证:平面;(2)求二面角的正切值.
- 有一个正四面体,它的棱长为a,现用一张圆型的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 .
- 已知正△ABC的边长为23,则到三个顶点的距离都为1的平面有______个.
- (本小题满分12分)如图,在四棱锥中,底面四边长为1的菱形,,,,为的中点.(Ⅰ)求异面直线AB与MD所成角的大小;(Ⅱ)求点B...
- 高为的四棱锥-的底面是边长为1的正方形,点、、、、均在半径为1的同一球面上,则底面的中心与顶点之间的距离为______________...
- 空间内五个点中的任意三点都不共线,由这五个点为顶点只构造出四个三棱锥,则这五个点最多可以确定________个平面.
- 一个多面体的直观图和三视图如图所示,其中分别是的中点,是上的一动点.(1)求证:(2)当时,在棱上确定一点,使得//平面,...
- 在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1;类比到空间,在长方体中,一条对...