本试题 “已知抛物线y=ax2+bx在第一象限内与直线x+y=4相切.(Ⅰ)用b表示a,并求b的范围;(Ⅱ)设此抛物线与x轴所围成的图形的面积为S,求S的最大值及此时a、b的值.” 主要考查您对函数的极值与导数的关系
定积分的简单应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的极值与导数的关系
- 定积分的简单应用
极值的定义:
(1)极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点;
(2)极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0),就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点。
极值的性质:
(1)极值是一个局部概念,由定义知道,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小;
(2)函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个;
(3)极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点,而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
判别f(x0)是极大、极小值的方法:
若x0满足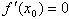 ,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点,
,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点, 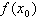 是极值,并且如果
是极值,并且如果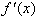 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果
在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
求函数f(x)的极值的步骤:
(1)确定函数的定义区间,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值。
对函数极值概念的理解:
极值是一个新的概念,它是研究函数在某一很小区域时给出的一个概念,在理解极值概念时要注意以下几点:
①按定义,极值点x0是区间[a,b]内部的点,不会是端点a,b(因为在端点不可导).如图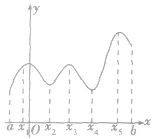
②极值是一个局部性概念,只要在一个小领域内成立即可.要注意极值必须在区间内的连续点取得.一个函数在定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一个点的极大值,也就是说极大值与极小值没有必然的大小关系,即极大值不一定比极小值大,极小值不一定比极大值小,如图.
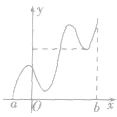
③若fx)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值.
④若函数f(x)在[a,b]上有极值且连续,则它的极值点的分布是有规律的,相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点,一般地,当函数f(x)在[a,b]上连续且有有
限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的,
⑤可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点,不可导的点也可能是极值点,也可能不是极值点,
定积分的简单应用:
1、求几何图形的面积:在直角坐标系中,由曲线f(x),直线x=a,x=b(a<b)和x轴围成的曲边梯形的面积,当对应的曲边梯形位于x轴上方时,定积分的取值为正值;当对应的曲边梯形位于x轴下方时,定积分的取值为负值;当位于x轴上方的曲边梯形面积等于位于x轴下方的曲线梯形面积时,定积分的值为0.
2、变速运动问题:如果变速运动的物体的速度v关于时间t的函数是v=v(t)(v(t)≥0),那么物体从时刻t=a到t=b所经过的路程为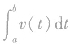 如果变速运动的物体的速度v关于时间t的函数是v=v(t)
如果变速运动的物体的速度v关于时间t的函数是v=v(t)
(v(t)≤0),那么物体从时刻t=a到t=b所经过的路程为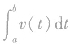 。
。
求定积分的方法:
方法1:用定义求定积分的一般步骤:
(1)分割:n等分区间[a,b];
(2)近似代替:取点ξi∈[xi-1,xi];
(3)求和:
(4)取极限:
方法2:用所求定积分表示的几何意义求积分
当定积分表示的面积容易求时,则利用定积分的几何意义求积分.
与“已知抛物线y=ax2+bx在第一象限内与直线x+y=4相切.(Ⅰ)用b表...”考查相似的试题有:
- 已知函数.(Ⅰ)求函数的单调区间;(Ⅱ)若在内恒成立,求实数的取值范围.(Ⅲ),求证:.
- 求limx→0ex-e-x-2xx-sinnx的值.
- 已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,则下列说法中正确结论的序号为___...
- 函数y=1x2+1在x=l处的切线方程是______.
- 已知函数(其中e为自然对数的底数)(Ⅰ)判断的奇偶性;(Ⅱ)在上求函数的极值;
- 设函数;(Ⅰ)求证:函数在上单调递增;(Ⅱ)设,若直线PQ∥x轴,求P,Q两点间的最短距离.
- 若实数a≠0,函数f(x)=-2ax3-ax2+12ax+1,g(x)=2ax2+3.(1)令h(x)=f(x)-g(x),求函数h(x)的极值;(2)若在区间...
- 设函数.(1)若是函数的一个极值点,试求出关于的关系式(用表示),并确定的单调区间;(2)在(1)的条件下,设,函数.若...
- 函数f(x)=x3-3x2+1在x=( )处取得极小值。
- 若函数y=cosx(0≤x≤2π)的图象与直线y=1围成一个封闭的平面图形,则这个图形的面积为( ) A.2 B.4 C.π D.2π