本试题 “在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与...” 主要考查您对余弦定理
点到直线的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 余弦定理
- 点到直线的距离
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: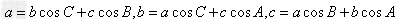
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: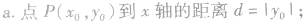
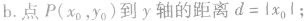
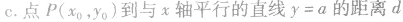

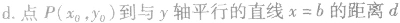
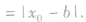
发现相似题
与“在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水...”考查相似的试题有:
- 锐角△ABC中,如果a=2,b=3,那么c的范围是( )A.1<c<5B.1<c<5C.5<c<13D.1<c<13
- ABC的三个内角A、B、C所对边长分别为a、b、c,设向量=(a+b,c),=(a+c,b-a),若,则角B的大小为 .
- 在锐角中,角的对边分别为,已知(1)求角;(2)若,求面积的最大值.
- 圆(x-3)2+(y+4)2=1关于直线x+y=0对称的圆的方程是( )A.(x+3)2+(y-4)2=1B.(x-4)2+(y+3)2=1C.(x+4)2+(y-3)...
- 设直线3x+4y-5=0与圆C1:交于A,B两点, 若圆C2的圆心在线段AB上, 且圆C2与圆C1相切, 切点在圆C1的劣弧上, 则圆C2的半径的最...
- (本小题9分)设直线3x+y+=0与圆x2+y2+x-2y=0相交于P、Q两点,O为坐标原点,若OPOQ,求的值.
- 若直线与曲线有两个不同的交点,实数的取值范围
- 设椭圆上一点P到其左焦点的距离为3,到右焦点的距离为1,则P到右准线的距离为[ ]A.6B.2C.D.
- 在曲线C1:(θ为参数)上求一点,使它到直线C2:(t为参数)的距离最小,并求出该点坐标和最小距离。
- 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)...