本试题 “若函数y=1x2+2x+m的自变量x的取值范围为一切实数,则m的取值范围为( )A.m≤1B.m=1C.m>1D.m<1” 主要考查您对完全平方公式
反比例函数的定义
一元二次方程根的判别式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 完全平方公式
- 反比例函数的定义
- 一元二次方程根的判别式
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。叫做完全平方公式.为了区别,我们把前者叫做两数和的完全平方公式,后者叫做两数差的完全平方公式。
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2。
(1)公式中的a、b可以是单项式,也就可以是多项式。
(2)不能直接应用公式的,要善于转化变形,运用公式。
该公式是进行代数运算与变形的重要的知识基础,是因式分解中常用到的公式。该知识点重点是对完全平方公式的熟记及应用。难点是对公式特征的理解(如对公式中积的一次项系数的理解)。
结构特征:
1.左边是两个相同的二项式相乘,右边是三项式,是左边二项式中两项的平方和,加上或减去这两项乘积的2倍;
2.左边两项符号相同时,右边各项全用“+”号连接;
左边两项符号相反时,右边平方项用“+”号连接后再“-”两项乘积的2倍(注:这里说项时未包括其符号在内);
3..公式中的字母可以表示具体的数(正数或负数),也可以表示单项式或多项式等数学式.
记忆口诀:首平方,尾平方,2倍首尾。
使用误解:
①漏下了一次项;
②混淆公式;
③运算结果中符号错误;
④变式应用难于掌握。
注意事项:
1、左边是一个二项式的完全平方。
2、右边是二项平方和,加上(或减去)这两项乘积的二倍,a和b可是数,单项式,多项式。
3、不论是还是,最后一项都是加号,不要因为前面的符号而理所当然的以为下一个符号。
完全平方公式的基本变形:
(一)、变符号
例:运用完全平方公式计算:
(1)(-4x+3y)2
(2)(-a-b)2
分析:本例改变了公式中a、b的符号,以第二小题为例,处理该问题最简单的方法是将这个式子中的(-a)看成原来公式中的a,将(-b)看成原来公式中的b,即可直接套用公式计算。
解答:
(1)16x2-24xy+9y2
(2)a2+2ab+b2
(二)、变项数:
例:计算:(3a+2b+c)2
分析:完全平方公式的左边是两个相同的二项式相乘,而本例中出现了三项,故应考虑将其中两项结合运用整体思想看成一项,从而化解矛盾。所以在运用公式时,(3a+2b+c)2可先变形为[(3a+2b)+c]2,直接套用公式计算。
解答:9a2+12ab+6ac+4b2+4bc+c2
(三)、变结构
例:运用公式计算:
(1)(x+y)(2x+2y)
(2)(a+b)(-a-b)
(3)(a-b)(b-a)
分析;本例中所给的均是二项式乘以二项式,表面看外观结构不符合公式特征,但仔细观察易发现,只要将其中一个因式作适当变形就可以了,即
(1)(x+y)(2x+2y)=2(x+y)2
(2) (a+b)(-a-b)=-(a+b)2
(3) (a-b)(b-a)=-(a-b)2
一般地,函数 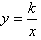 (k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
(k是常数,k≠0)叫做反比例函数,自变量x的取值范围是x≠0的一切实数,函数值的取值范围也是一切非零实数。
注:
(1)因为分母不能为零,所以反比例函数函数的自变量x不能为零,同样y也不能为零;
(2)由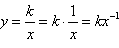 ,所以反比例函数可以写成
,所以反比例函数可以写成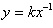 的形式,自变量x的次数为-1;
的形式,自变量x的次数为-1;
(3)在反比例函数中,两个变量成反比例关系,即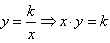 ,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
,因此判定两个变量是否成反比例关系,应看是否能写成反比例函数的形式,即两个变量的积是不是一个常数。
表达式:
x是自变量,y是因变量,y是x的函数
自变量的取值范围:
①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;
②函数y的取值范围也是任意非零实数。
反比例函数性质:
①反比例函数的表达式中,等号左边是函数值y,等号右边是关于自变量x的分式,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式;
②反比例函数表达式中,常数(也叫比例系数)k≠0是反比例函数定义的一个重要组成部分;
③反比例函数 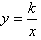 (k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
(k是常数,k≠0)的自变量x的取值范围是不等式0的任意实数,函数值y的取值范围也是非零实数。
一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac。
定理1 ax2+bx+c=0(a≠0)中,△>0
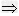 方程有两个不等实数根;
方程有两个不等实数根;定理2 ax2+bx+c=0(a≠0)中,△=0
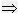 方程有两个相等实数根;
方程有两个相等实数根;定理3 ax2+bx+c=0(a≠0)中,△<0
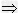 方程没有实数根。
方程没有实数根。根的判别式逆用(注意:根据课本“反过来也成立”)得到三个定理。
定理4 ax2+bx+c=0(a≠0)中,方程有两个不等实数根
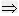 △>0;
△>0;定理5 ax2+bx+c=0(a≠0)中,方程有两个相等实数根
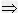 △=0;
△=0;定理6 ax2+bx+c=0(a≠0)中,方程没有实数根
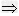 △<0。
△<0。注意:(1)再次强调:根的判别式是指△=b2-4ac。
(2)使用判别式之前一定要先把方程变化为一般形式,以便正确找出a、b、c的值。
(3)如果说方程,即应当包括有两个不等实根或有两相等实根两种情况,此时b2-4ac≥0切勿丢掉等号。
(4)根的判别式b2-4ac的使用条件,是在一元二次方程中,而非别的方程中,因此,要注意隐含条件a≠0。
根的判别式有以下应用:
①不解一元二次方程,判断根的情况。
②根据方程根的情况,确定待定系数的取值范围。
③证明字母系数方程有实数根或无实数根。
④应用根的判别式判断三角形的形状。
⑤判断当字母的值为何值时,二次三项是完全平方式。
⑥可以判断抛物线与直线有无公共点。
⑦可以判断抛物线与x轴有几个交点。
⑧利用根的判别式解有关抛物线
 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。与“若函数y=1x2+2x+m的自变量x的取值范围为一切实数,则m的取值...”考查相似的试题有:
- 若a+b=10,ab=5,则a2+b2的值为( ) A.100 B.126 C.441 D.90
- 已知x2-2mx+16是一个完全平方式,则m=( )。
- 下列计算中,正确的是( )A.(-2x-y)(2x-y)=y2-4x2B.x4+x4=x8C.(2m-n)2=4m2-2mn+n2D.6a-5a=1
- 下列结论正确的是[ ]A、如-, 则a
- 已知点A是反比例函数图象上的一点.若垂直于轴,垂足为,则的面积 .
- 已知y与x成正比例,z与y成反比例,则z与x之间的关系为( ) A.成正比例 B.成反比例 C.既成正比例又成反比例 D.既不成正比...
- 若函数与的图象有一个交点是(,2),则另一个交点坐标是 。
- 函数的图象如图所示,那么函数的图象大致是( )
- 当x为何有理数时,代数式9x2+23x-2的值恰为两个连续正偶数的乘积?
- 如果a为实数,并且方程x2-2-ax+(a-1)24=0有实根,那么a2009+a2010的值为( )A.-2B.0C.2D.不能确定