点到直线的距离：

由点向直线引垂线，这一点到垂足之间的距离。

点到平面的距离：

由点向平面引垂线，这点到垂足之间的距离，就叫做点到平面的距离。

求点面距离常用的方法：

(1)直接利用定义
①找到（或作出）表示距离的线段；
②抓住线段（所求距离）所在三角形解之．
(2)利用两平面互相垂直的性质如果已知点在已知平面的垂面上，则已知点到两平面交线的距离就是所求的点面距离．
(3)体积法其步骤是：①在平面内选取适当三点和已知点构成三棱锥；②求出此三棱锥的体积V和所取三点构成三角形的面积S；③由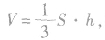求出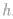．这种方法的优点是不必作出垂线即可求点面距离，难点在于如何构造合适的三棱锥以便于计算．
(4)转化法：将点到平面的距离转化为直线与平面的距离来求．
(5)向量法：