本试题 “设函数f(x)=3sinθ3x3+cosθ2x2+4x-1,其中θ∈[0, 5π6],则导数f'(-1)的取值范围( )A.[3,6]B.[3, 4+3]C.[4-3, 6]D.[4-3, 4+3]” 主要考查您对函数的定义域、值域
已知三角函数值求角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
- 已知三角函数值求角
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则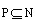 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如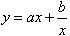 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
反三角函数的定义:
(1)反正弦:在闭区间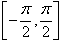 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中x∈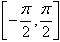 ,且a=sinx;
,且a=sinx;
注意arcsina表示一个角,这个角的正弦值为a,且这个角在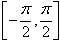 内(-1≤a≤1)。
内(-1≤a≤1)。
(2)反余弦:在闭区间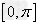 上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
上,符合条件cosx=a(-1≤a≤1)的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x∈[0,π],且a=cosx。
(3)反正切:在开区间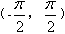 内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈
内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中x∈ ,且a=tanx。
,且a=tanx。
反三角函数的性质:
(1)sin(arcsina)=a(-1≤a≤1),cos(arccosa)=a(-1≤a≤1),
tan(arctana)=a;
(2)arcsin(-a)=-arcsina,arccos(-a)=π-arccosa,arctan(-a)=-arctana;
(3)arcsina+arccosa=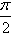 ;
;
(4)arcsin(sinx)=x,只有当x在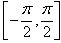 内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
内成立;同理arccos(cosx)=x只有当x在闭区间[0,π]上成立。
已知三角函数值求角的步骤:
(1)由已知三角函数值的符号确定角的终边所在的象限(或终边在哪条坐标轴上);
(2)若函数值为正数,先求出对应锐角α1,若函数值为负数,先求出与其绝对值对应的锐角α1;
(3)根据角所在象限,由诱导公式得出0~2π间的角,如果适合条件的角在第二象限,则它是π-α1;如果适合条件的角在第三象限,则它是π+α1;在第四象限,则它是2π-α1;如果是-2π到0的角,在第四象限时为-α1,在第三象限为-π+α1,在第二象限为-π-α1;
(4)如果要求适合条件的所有角,则利用终边相同的角的表达式来写出。
与“设函数f(x)=3sinθ3x3+cosθ2x2+4x-1,其中θ∈[0, 5π6],则导数...”考查相似的试题有:
- 函数y=f(x)是定义在区间(-∞,-12]∪[12,+∞)上的奇函数,当x≥12时,f(x)=2x-x2.(1)求x≤-12时,f(x)的解析式;(2)若...
- 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的...
- 已知函数f(t)=log2t,t∈[2,8](1)求f(t)的值域G(2)若对G内的所有实数x,不等式-x2+2mx-m2+2m≤1恒成立,求实数m的取值范...
- 函数f(x)=1x-5+lg(x2-4)的定义域为______.
- 函数的值域为( )。
- 定义在R上的函数且当时,.则等于 ( )A.B.C.D.
- 关于函数y=f(x),有下列命题:①若a∈[﹣2,2],则函数f(x)=的定义域为R;②若f(x)=(x2﹣3x+2),则f(x)的单调增区间为...
- 已知函数f(x)=4cosxsin(x+π6)-1.(1)求f(x)的最小正周期:(2)已知p:θ>π4,q:函数g(x)=(θ+1)x在R上为增函数,若p∧q为...
- 在△ABC中,若三边a,b,c成等差数列,sinA,sinB,sinC成等比数列,则△ABC的形状是______三角形.(填写“等腰”、“等边”、“直...
- 化简:的值为( ) A.1 B.sinx+cosx C.sinxcosx D.1+sinxcosx