本试题 “已知函数(且).(1)当时,求证:在上单调递增;(2)当且时,求证:.” 主要考查您对导数的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 导数的运算
常见函数的导数:
(1)C′=0 ;(2)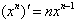 ;(3)
;(3)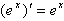 ;(4)
;(4) ;(5)
;(5)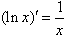 ;(6)
;(6)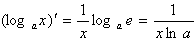 ;(7)
;(7)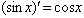 ;(8)
;(8)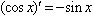
导数的四则运算:
(1)和差: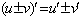
(2)积: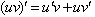
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: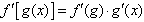
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
发现相似题
与“已知函数(且).(1)当时,求证:在上单调递增;(2)当且时,...”考查相似的试题有:
- 已知函数f(x)=mxm-n的导数为f′(x)=8x3,则mn=______.
- ,则 ( )A.B.C.D.
- ,若,则的值等于A.B.C.D.
- 已知函数f(x)=2ln3x+8x,则的值为[ ]A.﹣20B.﹣10C.10D.20
- 将函数f(x)=ex展开为x的幂级数,并求出收敛区间.(e=2.718为自然对数的底)
- 已知函数定义域为(),设.(1)试确定的取值范围,使得函数在上为单调函数;(2)求证:;(3)求证:对于任意的,总存在,满足,...
- 函数的导数=[ ]A.B.C.D.
- 已知函数的对称中心为M,记函数的导函数为,的导函数为,则有.若函数,则可求得: .
- 已知函数f(x)=x3+2ax2+x(a>0),则f '(1)的最小值为( ).
- 已知函数f(x)的导数为f'(x),且满足f(x)=3x2+2xf'(1),则f'(3)=( )A.9B.6C.-6D.20