返回

高中三年级数学

首页
首页 高中三年级数学知识 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等） 简单曲线的极坐标方程 椭圆的参数方程 试题正文
  • 解答题
    （选做题）已知曲线C1的参数方程是，以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为。
    （1）求点A，B，C，D的直角坐标；
    （2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围。
    本题信息：2012年高考真题数学解答题难度较难 来源:刘佩
  • 本题答案
    查看答案
本试题 “（选做题）已知曲线C1的参数方程是，以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依...” 主要考查您对

正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

简单曲线的极坐标方程

椭圆的参数方程

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）
  • 简单曲线的极坐标方程
  • 椭圆的参数方程

正弦函数和余弦函数的图象：正弦函数y=sinx（x∈R）和余弦函数y=cosx（x∈R）的图象分别叫做正弦曲线和余弦曲线，

1．正弦函数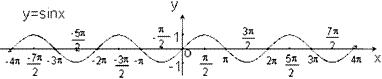

2．余弦函数

函数图像的性质
正弦、余弦函数图象的性质：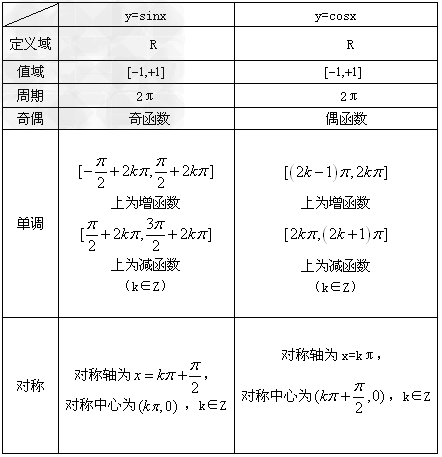

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当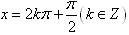时，y取最大值1，
当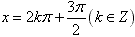时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。




正弦、余弦函数图象的性质：


由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当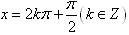时，y取最大值1，
当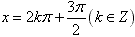时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。


曲线的极坐标方程的定义：

一般地，在极坐标系中，如果平面曲线C上任意一点的极坐标中至少有一个满足方程f（ρ，θ）=0，并且坐标适合方程f（ρ，θ）=0的点都在曲线上，那么方程f（ρ，θ）=0叫做曲线C的极坐标方程。


求曲线的极坐标方程的常用方法：

直译法、待定系数法、相关点法等。

圆心为（α，β）（a＞0），半径为a的圆的极坐标方程为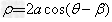，此圆过极点O。

直线的极坐标方程：

直线的极坐标方程是ρ=1/（2cosθ＋4sinθ）。

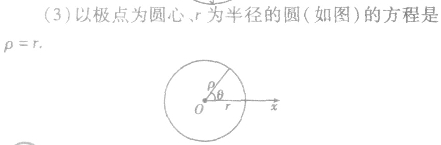
圆的极坐标方程：


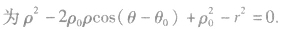
这是圆在极坐标系下的一般方程。
 
过极点且半径为r的圆方程：
 
 

椭圆的参数方程：

椭圆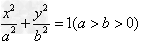的参数方程是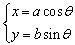，θ∈[0，2π）。


椭圆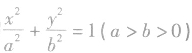的参数方程的理解：

如图，以原点为圆心，分别以a，b（a>b>0）为半径作两个圆，点B是大圆半径OA与小圆的交点，过点A作AN⊥Ox，垂足为N，过点B作BM⊥AN，垂足为M，求当半径OA绕点O旋转时，点M的横坐标与点A的横坐标相同，点M的纵坐标与点B的纵坐标相同．而A、B的坐标可以通过引进参数建立联系．设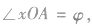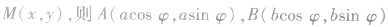，由已知得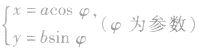，即为点M的轨迹参数方程，消去参数得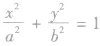，即为点M的轨迹普通方程。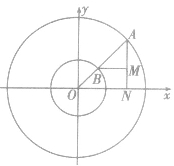
(1)参数方程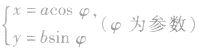，是椭圆的参数方程；
(2)在椭圆的参数方程中，常数a、b分别是椭圆的长半轴长和短半轴长．a>b,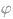称为离心角，规定参数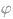的取值范围是[0，2π）;
(3)焦点在y轴的参数方程为


发现相似题
与“（选做题）已知曲线C1的参数方程是，以坐标原点为极点，x轴的...”考查相似的试题有：