本试题 “以点(1,0)为圆心,且与直线2x+y=1相切的圆方程是______.” 主要考查您对圆的标准方程与一般方程
圆的切线方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 圆的标准方程与一般方程
- 圆的切线方程
圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为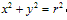 。
。
圆的一般方程:
圆的一般方程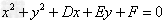
当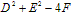 >0时,表示圆心在
>0时,表示圆心在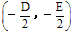 ,半径为
,半径为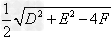 的圆;
的圆;
当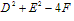 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.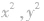 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如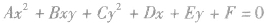 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即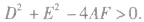
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
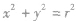 |
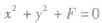 |
| 过原点 |
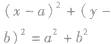 |
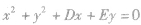 |
| 圆心在x轴上 |
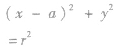 |
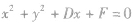 |
| 圆心在y轴上 |
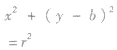 |
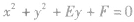 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
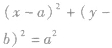 |
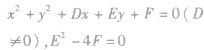 |
|
与x,y轴都相切 |
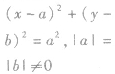 |
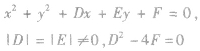 |
| 圆心在x轴上且过原点 |
 |
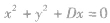 |
| 圆心在y轴上且过原点 |
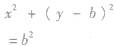 |
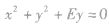 |
圆的切线方程:
1、已知圆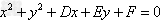 ,
,
(1)若已知切点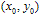 在圆上,则切线只有一条,其方程是
在圆上,则切线只有一条,其方程是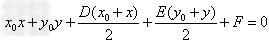 ;
;
(2)当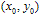 圆外时,
圆外时,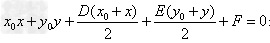 表示过两个切点的切点弦方程。
表示过两个切点的切点弦方程。
(3)过圆外一点的切线方程可设为 ,再利用相切条件求k,这时必有两条切线。
,再利用相切条件求k,这时必有两条切线。
(4)斜率为k的切线方程可设为y=kx+b,再利用相切条件求b,必有两条切线。
2、已知圆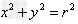 ,
,
(1)过圆上的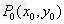 点的切线方程为
点的切线方程为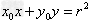 ;
;
(2)斜率为k的圆的切线方程为 。
。
圆的切线方程的求法:
①代数法:设出切线方程,利用切线与圆仅有一个交点,将直线方程代入圆的方程,从而△=0,可求解;
②几何法利用几何特征:圆心到切线的距离等于圆的半径,可求解.
过定点的圆的切线方程:
①过圆上一点的切线方程:
与圆 的切线方程是
的切线方程是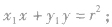
与圆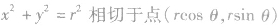 的切线方程是
的切线方程是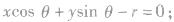
与圆 的切线方程是
的切线方程是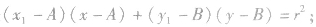
与圆 的切线方程是
的切线方程是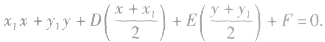
②过圆外一点的切线方程:设 外一点,求过P0点的圆的切线.
外一点,求过P0点的圆的切线.
方法l:设切点是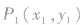 ,解方程组
,解方程组

方法2:设切线方程是
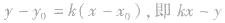
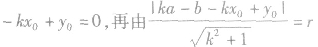 ,再由
,再由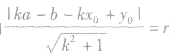 求出待定系数k,就可写出切线方程.
求出待定系数k,就可写出切线方程.特别提醒:一般说来,方法2比较简便,但应注意,可能遗漏k不存在的切线.因此,当解出的k值唯一时,应观察图形,看是否有垂直于x轴的切线.
与“以点(1,0)为圆心,且与直线2x+y=1相切的圆方程是______.”考查相似的试题有:
- 若圆的圆心到直线的距离小于,则实数的取值范围是 .
- 已知圆与x轴切于A点,与y轴切于B点,设劣弧的中点为M,则过点M的圆C的切线方程是( )A.B.C.D.
- (附加题)本题满分20分如图,已知抛物线与圆相交于A、B、C、D四个点。(Ⅰ)求r的取值范围 (Ⅱ)当四边形ABCD的面积最大时,求...
- 若函数的图象在处的切线为, 则上的点到圆上的点的最近距离是 ( )A.B.C.D.1
- 已知点P(2,0)及圆C:x2+y2-6x+4y+4=0。(1)若直线l过点P且与圆心C的距离为1,求直线l的方程;(2)设过点P的直线l1与圆C...
- 如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过...
- 求与圆外切,且与直线相切于点的圆的方程.
- 以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是( )A.(x-1)2+(y+2)2=100B.(x-1)2+(y-2)2=100C.(x-1)2+(...
- M是圆+=4上一动点,N(3,0),则线段MN中点的轨迹方程是_________
- 要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是关径为6米的圆面,则需...