本试题 “设函数f(x)=x|x-a|+b(1) 求证:f(x)为奇函数的充要条件是a2+b2=0;(2)设常数b<22-3,求对任意x∈[0,1],f(x)<0的充要条件.” 主要考查您对充分条件与必要条件
函数的奇偶性、周期性
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 函数的奇偶性、周期性
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有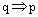 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且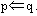 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
函数的奇偶性定义:
偶函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),则称函数f(x)为偶函数。
奇函数:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)是奇函数。
函数的周期性:
(1)定义:若T为非零常数,对于定义域内的任一x,使f(x+T)=f(x)恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
周期函数定义域必是无界的。
(2)若T是周期,则k·T(k≠0,k∈Z)也是周期,所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期,如常函数f(x)=C。
奇函数与偶函数性质:
(1)奇函数与偶函数的图像的对称性:奇函数的图像关于原点对称,偶函数的图像关于y轴对称。
(3)在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数。
注:定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
1、函数是奇函数或偶函数的前提定义域必须关于原点对称;定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件.
2、函数的周期性 令a , b 均不为零,若:
(1)函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
(2)函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
(3)函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
(4)函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
==> 函数最小正周期 T=|2a|
(5)函数y = f(x) 存在 f(x + a) = 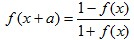 ==> 函数最小正周期 T=|4a|
==> 函数最小正周期 T=|4a|
与“设函数f(x)=x|x-a|+b(1) 求证:f(x)为奇函数的充要条件...”考查相似的试题有:
- 下列命题是真命题的是( )A.的充要条件B.的充分条件C.D.若为真命题,则为真
- 已知为实数,条件:,条件:,则是的[ ]A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件
- 已知α、β均为锐角,若p:sinα<sin(α+β),q:α+β<π2,则p是q的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D...
- 若a,b为实数,则“0<ab<1”是或的[ ]A、充分而不必要条件B、必要而不充分条件C、充分必要条件D、既不充分也不必要条件
- 写出二次函数y=ax2+bx+c(a≠0)的图像与x轴没有交点的一个充分不必要条件是( )。
- [2014·徐州检测]用分析法证明:欲使①A>B,只需②C
- 设a∈R,f(x)=a-22x+1(x∈R)为奇函数,则a=______.
- 已知函数f(x)=1-42ax+a(a>0且a≠1)是定义在(-∞,+∞)上的奇函数.(1)求a的值;(2)当x∈(0,1]时,t•f(x)≥2x-2恒成立...
- 已知是定义在R上的奇函数,且当时,f(x)=log2x求的解析式。
- 已知定义域为R的函数y=f(x)满足f(-x)=-f(x+4),当x>2时,f(x)单调递增,若x1+x2<4且(x1-2)(x2-2)<0,则f(x1...