本试题 “设指数函数f(x)=ax(a>0且a≠1),则下列等式不正确的是( ) A.f(x+y)=f(x)•f(y) B.f[(xy)n]=[f(x)]n•[f(y)]n C.f(x-y)= D.f(nx)=[f...” 主要考查您对指数与指数幂的运算(整数、有理、无理)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数与指数幂的运算(整数、有理、无理)
n次方根的定义:
一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*。
分数指数幂的意义:
(1)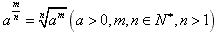 ;
;
(2) ;
;
(3)0的正分数指数幂等于0,0的负分数指数幂没有意义。
n次方根的性质:
(1)0的n次方根是0,即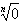 =0(n>1,n∈N*);
=0(n>1,n∈N*);
(2)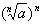 =a(n∈N*);
=a(n∈N*);
(3)当n为奇数时,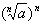 =a;当n为偶数时,
=a;当n为偶数时,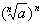 =|a|。
=|a|。
幂的运算性质:
(1)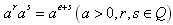 ;
;
(2) ;
;
(3)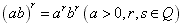 ;
;
注意:一般地,无理数指数幂 (a>0,α是无理数)是一个确定的实数,上述有理指数幂的运算性质,对于无理指数幂都适用。
(a>0,α是无理数)是一个确定的实数,上述有理指数幂的运算性质,对于无理指数幂都适用。
发现相似题
与“设指数函数f(x)=ax(a>0且a≠1),则下列等式不正确的是( ...”考查相似的试题有:
- 化简求值:(1) 已知,求;(2).
- 若,则A.B.C.D.
- 若函数在上有意义,则实数的取值范围是_ ___.
- 已知函数,R.则对任意实数,函数不可能( )A.是奇函数B.既是奇函数,又是偶函数C.是偶函数D.既不是奇函数,又不是偶函数
- 幂函数的图象经过点),则其解析式是 .
- 将写为根式,则正确的是( ) A. B. C. D.
- 若0<a<1,π2<x<π,则(a-x)2x-a-cosx|cosx|+1-axax-1的值是______.
- 化简:+π=( ) A.4 B.2π-4 C.2π-4或4 D.-2π
- 函数的图象恒过点A,若直线:经过点A,则坐标原点O到直线的距离的最大值为 。
- (文)(1)若-2x2+5x-2>0,化简:4x2-4x+1+2|x-2|(2)求关于x的不等式(k2-2k+52)x<(k2-2k+52)1ˉx的解集.