本试题 “化简求值:(1) 已知,求;(2).” 主要考查您对指数与指数幂的运算(整数、有理、无理)
对数与对数运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 指数与指数幂的运算(整数、有理、无理)
- 对数与对数运算
n次方根的定义:
一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*。
分数指数幂的意义:
(1)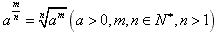 ;
;
(2) ;
;
(3)0的正分数指数幂等于0,0的负分数指数幂没有意义。
n次方根的性质:
(1)0的n次方根是0,即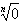 =0(n>1,n∈N*);
=0(n>1,n∈N*);
(2)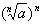 =a(n∈N*);
=a(n∈N*);
(3)当n为奇数时,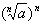 =a;当n为偶数时,
=a;当n为偶数时,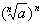 =|a|。
=|a|。
幂的运算性质:
(1)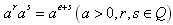 ;
;
(2) ;
;
(3)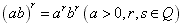 ;
;
注意:一般地,无理数指数幂 (a>0,α是无理数)是一个确定的实数,上述有理指数幂的运算性质,对于无理指数幂都适用。
(a>0,α是无理数)是一个确定的实数,上述有理指数幂的运算性质,对于无理指数幂都适用。
对数的定义:
如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记做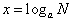 ,其中a叫做对数的底数,N叫做真数。
,其中a叫做对数的底数,N叫做真数。
通常以10为底的对数叫做常用对数,记做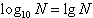 ;
;
以无理数e=2.71828…为底的对数叫做自然对数,记做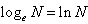 。
。
由定义知负数和0没有对数。
常用对数:
以10为底的对数叫做常用对数, 。
。
自然对数:
以e为底的对数叫做自然对数,e是无理数,e≈-2. 718 28, 。
。
对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
(1)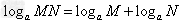 ;
;
(2)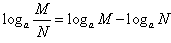 ;
;
(3) ;
;
(4) 。
。
对数的恒等式:
(1)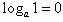 ;(2)
;(2)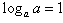 ;
;
(3)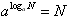 ;(4)
;(4) ;
;
(5)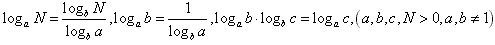 。
。
对数的换底公式及其推论:
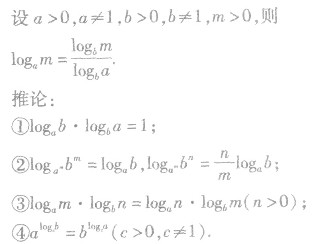
对数式的化简与求值:
(1)化同底是对数式变形的首选方向,其中经常用到换底公式及其推论.
(2)结合对数定义,适时进行对数式与指数式的互化.
(3)利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化,
发现相似题
与“化简求值:(1) 已知,求;(2).”考查相似的试题有:
- 计算:=
- 下列各计算中,正确的是[ ]A.B.C.D.
- 定义在R上的函数y=f(x)满足:①若x1<x2,则f(x1)>f(x2);②f(x1+x2-1)=f(x1)•f(x2),请写出符合条件的一个函数__...
- 已知函数的图象与直线图象相切,则
- 若函数y = (-3a + 3)·是指数函数 ,则( )A.a = 1或a =" 2"B.a =" 1"C.a =" 2"D.a>0且a≠ 1
- 函数y= ()的图象是( )
- 设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,令an=lgxn,则a1+a2+…+a99的值为( )。
- (1)计算:;(2)解方程:log3(6x-9)=3。
- 已知函数满足:,则;当时,则( )A.B.C.D.
- 函数的零点所在的大致范围是 ( )A.(1,2)B.(0,1)C.(,1)和(3,4)D.(2,+)