本试题 “给出下列几个命题:①若函数的定义域为,则一定是偶函数;②若函数是定义域为的奇函数,对于任意的都有,则函数的图象关于直线对称;③已知是函数定义域内的两个...” 主要考查您对函数的定义域、值域
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则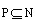 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如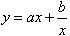 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
发现相似题
与“给出下列几个命题:①若函数的定义域为,则一定是偶函数;②若...”考查相似的试题有:
- 函数y=x2-2x-3x2+3x+2的值域是( )A.{y|y∈R且y≠1}B.{y|-4≤y<1}C.{y|y≠-4且y≠1}D.R
- 已知函数分别由下表给出,则满足f(g(x))>g(f(x))的x的值是______.x123g(x)321x123f(x)131
- 已知二次函数f(x)=ax2+bx+c(a,b,c∈R),当x∈(-∞,-2)∪(0,+∞)时,f(x)>0,当x∈(-2,0)时,f(x)<0,且对任意...
- 函数的定义域是(用区间表示)( )。
- 已知f(x)=1x-1.(1)求函数f(x)的定义域;(2)判断并用定义证明函数f(x)的单调性.
- 函数y=1-(12)x的定义域是______.
- 函数f(x)的定义域是[-1,2],则函数y=f(log2(1-2x))的定义域是 ______.
- 函数的定义域为( )。
- 函数的定义域是( )
- 关于狄利克雷函数的叙述错误的是 ( )A.的值域是B.是偶函数C.是奇函数D.的定义域是