已知函数f（x）=x2+2x-4，(x＞0)，g（x）和f（x）的图象关于原点对称．（I）求函数g（x）的解析式；（II）试判断g（x）在（,高中,数学试题,函数图象考点,函数解析式的求解及其常用方法考点,函数的单调性与导数的关系考点,好技网

解答题
已知函数f（x）=x2+
2
x
-4，(x＞0)，g（x）和f（x）的图象关于原点对称．
（I）求函数g（x）的解析式；
（II）试判断g（x）在（-1，0）上的单调性，并给予证明；
（III）将函数g（x）的图象向右平移a（a＞0）个单位，再向下平移b（b＞0）个单位，若对于任意的a，平移后gf（x）和f（x）的图象最多只有一个交点，求b的最小值．

本题信息：数学解答题难度较难来源:未知
本题答案
查看答案

本试题 “已知函数f（x）=x2+2x-4，(x＞0)，g（x）和f（x）的图象关于原点对称．（I）求函数g（x）的解析式；（II）试判断g（x）在（-1，0）上的单调性，并给予证明；...” 主要考查您对
函数图象

函数解析式的求解及其常用方法

函数的单调性与导数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

函数图象
函数解析式的求解及其常用方法
函数的单调性与导数的关系

定义：

点集{（x，y）|y=f（x）}叫做函数y=f（x）的图像。

函数图像的画法：

（1）描点法：
一般我们选择一些特殊点（包括区间端点、最值点、极值点、函数图像与坐标轴的交点等）。
（2）用函数的性质画图
一般我们选择先确定函数的定义域，再看函数是否具有周期性和对称性、奇偶性，这样我们就可以只画出部分图像，之后根据性质直接得到其余部分的图像，然后判断单调性，确定特殊点或渐近线，进而得到函数的大致图像。
（3）通过图像变换画图
（一）平移变化：
Ⅰ水平平移：函数y=f（x+a）的图像可以把函数y=f（x）的图像沿x轴方向向左（a＞0）或向右（a＜0）平移|a|个单位即可得到；
Ⅱ竖直平移：函数y=f（x+a）的图像可以把函数y=f（x）的图像沿x轴方向向上（a＞0）或向下（a＜0）平移|a|个单位即可得到．
（二）对称变换：
Ⅰ函数y=f（-x）的图像可以将函数y=f（x）的图像关于y轴对称即可得到；
Ⅱ函数y=-f（x）的图像可以将函数y=f（x）的图像关于x轴对称即可得到；
Ⅲ函数y=-f（-x）的图像可以将函数y=f（x）的图像关于原点对称即可得到；
Ⅳ函数y=f^-1（x）的图像可以将函数y=f（x）的图像关于直线y=x对称得到．

函数图像的判断：

这里主要是抽象函数的图像，借助函数的对称性、周期性及单调性确定函数的图像；另外借助导数，就是函数在某点处的切线斜率的变化，体现在函数的图像上就是增长的快还是慢来确定函数的图像。

常用结论：

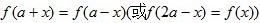（1）若函数y=f(x)定义域内任一x的值都满足f(a+x)=f(b-x)，则y=f(x)的图像关于直线成轴对称图形；特别地，y=f(x)满足恒成立，则y=f(x)的图像关于直线x=a成轴对称图形；
（2）函数y=f(x)的图像关于直线x=a及x=b对称，则y=f(x)是周期函数，且2|b-a|是它的一个周期。

函数解析式的常用求解方法：

（1）待定系数法：（已知函数类型如：一次、二次函数、反比例函数等）：若已知f（x）的结构时，可设出含参数的表达式，再根据已知条件，列方程或方程组，从而求出待定的参数，求得f（x）的表达式。待定系数法是一种重要的数学方法，它只适用于已知所求函数的类型求其解析式。
（2）换元法（注意新元的取值范围）：已知f（g（x））的表达式，欲求f（x），我们常设t=g（x），从而求得，然后代入f（g（x））的表达式，从而得到f（t）的表达式，即为f（x）的表达式。
（3）配凑法（整体代换法）：若已知f（g（x））的表达式，欲求f（x）的表达式，用换元法有困难时，（如g（x）不存在反函数）可把g（x）看成一个整体，把右边变为由g（x）组成的式子，再换元求出f（x）的式子。
（4）消元法（如自变量互为倒数、已知f（x）为奇函数且g（x）为偶函数等）：若已知以函数为元的方程形式，若能设法构造另一个方程，组成方程组，再解这个方程组，求出函数元，称这个方法为消元法。
（5）赋值法（特殊值代入法）：在求某些函数的表达式或求某些函数值时，有时把已知条件中的某些变量赋值，使问题简单明了，从而易于求出函数的表达式。

导数和函数的单调性的关系：

（1）若f′（x）>0在（a，b）上恒成立，则f（x）在（a，b）上是增函数，f′（x）>0的解集与定义域的交集的对应区间为增区间；
（2）若f′（x）<0在（a，b）上恒成立，则f（x）在（a，b）上是减函数，f′（x）<0的解集与定义域的交集的对应区间为减区间。

利用导数求解多项式函数单调性的一般步骤：

①确定f（x）的定义域；
②计算导数f′（x）；
③求出f′（x）=0的根；
④用f′（x）=0的根将f（x）的定义域分成若干个区间，列表考察这若干个区间内f′（x）的符号，进而确定f（x）的单调区间：f′（x）>0，则f（x）在对应区间上是增函数，对应区间为增区间；f′（x）<0，则f（x）在对应区间上是减函数，对应区间为减区间。

函数的导数和函数的单调性关系特别提醒：

若在某区间上有有限个点使f′(x)=0，在其余的点恒有f′（x）>0，则f(x)仍为增函数（减函数的情形完全类似）．即在区间内f′(x)>0是f(x)在此区间上为增函数的充分条件，而不是必要条件。

发现相似题

与“已知函数f（x）=x2+2x-4，(x＞0)，g（x）和f（x）的图象关于...”考查相似的试题有：