本试题 “若f(sinx)=3-cos2x,则f(cosx)=( ) A.3-cos2x B.3-sin2x C.3+cos2x D.3+sin2x” 主要考查您对函数解析式的求解及其常用方法
同角三角函数的基本关系式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数解析式的求解及其常用方法
- 同角三角函数的基本关系式
函数解析式的常用求解方法:
(1)待定系数法:(已知函数类型如:一次、二次函数、反比例函数等):若已知f(x)的结构时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得f(x)的表达式。待定系数法是一种重要的数学方法,它只适用于已知所求函数的类型求其解析式。
(2)换元法(注意新元的取值范围):已知f(g(x))的表达式,欲求f(x),我们常设t=g(x),从而求得 ,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
,然后代入f(g(x))的表达式,从而得到f(t)的表达式,即为f(x)的表达式。
(3)配凑法(整体代换法):若已知f(g(x))的表达式,欲求f(x)的表达式,用换元法有困难时,(如g(x)不存在反函数)可把g(x)看成一个整体,把右边变为由g(x)组成的式子,再换元求出f(x)的式子。
(4)消元法(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等):若已知以函数为元的方程形式,若能设法构造另一个方程,组成方程组,再解这个方程组,求出函数元,称这个方法为消元法。
(5)赋值法(特殊值代入法):在求某些函数的表达式或求某些函数值时,有时把已知条件中的某些变量赋值,使问题简单明了,从而易于求出函数的表达式。
同角三角函数的关系式:
(1)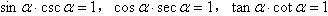 ;
;
(2)商数关系: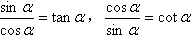 ;
;
(3)平方关系: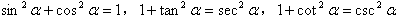 。
。
同角三角函数的基本关系的应用:
已知一个角的一种三角函数值,根据角的终边的位置利用同角三角函数的基本关系,可以求出这个角的其他三角函数值.
同角三角函数的基本关系的理解:
(1)在公式中,要求是同一个角,如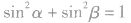 不一定成立.
不一定成立.
(2)上面的关系式都是对使它的两边具有意义的那些角而言的,如:基本三角关系式 。对一切α∈R成立;
。对一切α∈R成立;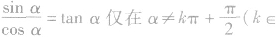 Z)时成立.
Z)时成立.
(3)同角三角函数的基本关系的应用极为为广泛,它们还有如下等价形式: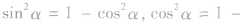

(4)在应用平方关系时,常用到平方根、算术平方根和绝对值的概念,应注意“±”的选取.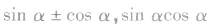 间的基本变形 三者通过
间的基本变形 三者通过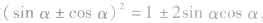 ,可知一求二,有关
,可知一求二,有关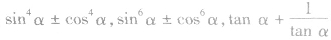 等化简都与此基本变形有广泛的联系,要熟练掌握。
等化简都与此基本变形有广泛的联系,要熟练掌握。
与“若f(sinx)=3-cos2x,则f(cosx)=( ) A.3-cos2x B.3-si...”考查相似的试题有:
- 已知f (x+1)=x2-3x+2,则f(1x)的解析表达式为______.
- 已知-π2<θ<π2,且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,在以下四个答案中,可能正确的是( )A.-3B.3或13C.-13...
- 函数f(x)=cos2x+sinx在区间[-π4,π4]上的最小值是( )A.2-12B.-1+22C.-1D.1-22
- 求函数y=-cos2x-4sinx+6的值域.
- 已知:tan(α+π4)=13,则(sinα-cosα)2cos2α等于( )A.3B.-3C.2D.-2
- 已知sinθ+cosθ=35,则sinθ•cosθ=______.
- 已知sinα+cosαsinα-cosα=3,则1sin2α-sinαcosα-cos2α=______.
- 证明:。
- 已知cos(π2+φ)=32,且|φ|<π2,则tanφ=( )A.-33B.33C.-3D.3
- 已知,,,则的值=________________.