本试题 “如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:(1)l是⊙O的切线;(2)PB平分∠ABD.” 主要考查您对不等式的定义及性质
简单曲线的极坐标方程
弦切角的性质
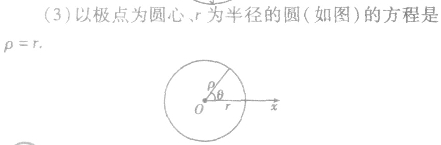
矩阵与变换
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 不等式的定义及性质
- 简单曲线的极坐标方程
- 弦切角的性质
- 矩阵与变换
不等式的定义:
一般地,用不等号表示不相等关系的式子叫做不等式,常见的不等号有“<”“>”“ ≤”“≥”及“≠”。
严格不等式的定义:
用“>"“<”连接的不等式叫做严格不等式。
非严格不等式的定义:
用“≤”和“≥”连接的不等式叫做非严格不等式.
特别提醒:a=b,a>b中,只要有一个成立,就有a≥b.
不等式的性质:
(1)如果a>b,那么b<a;如果b<a,那么a>b,即a>b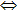 b<a;
b<a;
(2)如果a>b,b>c,那么a>c,即a>b,b>c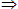 a>c;
a>c;
(3)如果a>b,那么a+c>b+c;
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac<bc;
(5)如果a>b,c>d,那么a+c>b+d;
(6)如果a>b>0,c>d>0,那么ac>bd;
(7)如果a>b>0,那么an>bn(n∈N,n≥2);
(8)如果a>b>0,那么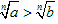 (n∈N,n≥2)。
(n∈N,n≥2)。
不等关系与不等式的区别:
不等关系强调的是量与量之间的关系,可以用符号“<…>…≤”“≥”来表示,也可以用语言表述;
而不等式则是用来表示不等关系的式子,可用“a>b”‘a<b”“a≥b a≤b”等式子来表示,不等关系是通过不等式来体现的.
不等式的分类:
①按成立的条件分:a.绝对不等式:不等式中的字母取任意实数值都恒成立的不等式叫做绝对不等式;b.条件不等式:不等式中的字母取某些允许值才能成立的不等式叫做条件不等式;c.矛盾不等式:不等式中的字母不论取何实数值都不能成立的不等式叫做矛盾不等式;
②按不等号开口方向分:a.同向不等式:不等号方向相同的两个不等式;b.异向不等式:不等号方向相反的两个不等式.
曲线的极坐标方程的定义:
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法:
直译法、待定系数法、相关点法等。
圆心为(α,β)(a>0),半径为a的圆的极坐标方程为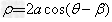 ,此圆过极点O。
,此圆过极点O。
直线的极坐标方程:
直线的极坐标方程是ρ=1/(2cosθ+4sinθ)。
圆的极坐标方程:

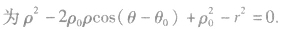

这是圆在极坐标系下的一般方程。


弦切角的定义:
顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。(弦切角就是切线与弦所夹的角)
如图所示,直线PT切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。
弦切角定理:
弦切角等于它所夹的弧所对的圆周角;
弦切角的度数等于它所夹的弧的圆心角的度数的一半。
弦切角定理证明:
设圆心为O,连接OC,OB,
∵∠TCB=90°-∠OCB∵∠BOC=180°-2∠OCB∴,∠BOC=2∠TCB(定理:弦切角的度数等于它所夹的弧所对的圆心角的度数的一半)
∵∠BOC=2∠CAB(同一弧所对的圆心角等于圆周角的两倍)
∴∠TCB=∠CAB(定理:弦切角的度数等于它所夹的弧的圆周角)|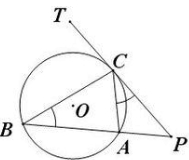
弦切角推论
若两弦切角所夹的弧相等,则这两个弦切角也相等.
弦切角定理的应用:
弦切角定理以及等弧对等角常用来证明角相等,由相似三角形常解决比例线段问题。
矩阵的定义:
由m×n个数排成的m行n列的表
称为m行n列矩阵(matrix),简称m×n矩阵。
特殊形式矩阵:
(1)n阶方阵:在矩阵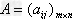 中,当m=n时,A称为n阶方阵;
中,当m=n时,A称为n阶方阵;
(2)行矩阵:只有一行的矩阵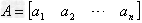 叫做行矩阵;
叫做行矩阵;
列矩阵:只有一列的矩阵,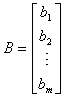 叫做列矩阵;
叫做列矩阵;
(3)零矩阵:元素都是零的矩阵称作零矩阵。
二阶矩阵与平面图形的变换:
(1)二阶矩阵的定义:由4个数a,b,c,d排成的正方形数表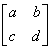 称为二阶矩阵;
称为二阶矩阵;
(2)几种特殊线性变换:主要有旋转变换、反射变换、伸压变换、投影变换、切变变换这几种。求经矩阵变换后的解析式常采用数形结合的方法,先观察是属于哪一种变换,然后利用解析几何中的相关点法(转移代入法)来解。
矩阵的运算律:
(1)矩阵的和(差):当两个矩阵A、B的维数相同时,将它们各位置上的元素加(减)所得到的矩阵称为矩阵A、B的和(差),记作: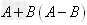 。
。
运算律:加法运算律: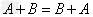 ;
;
加法结合律: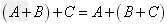 。
。
(2)数乘矩阵:矩阵与实数的积:设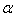 为任意实数,把矩阵A的所有元素与
为任意实数,把矩阵A的所有元素与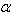 相乘得到的矩阵叫做矩阵A与实数
相乘得到的矩阵叫做矩阵A与实数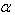 的乘积矩阵,记作:
的乘积矩阵,记作: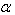 A。
A。
运算律:(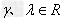 )
)
分配律: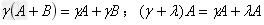 ;
;
结合律: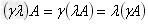 。
。
(3)矩阵的乘积:一般地,设A是m×k阶矩阵,B是k×n阶矩阵,设C为m×n矩阵,如果矩阵C中第i行第j列元素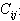 是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
运算律:
分配律: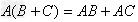 ;
;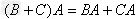 ;
;
结合律: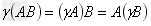 ;
;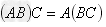 。
。
注:(1)交换律不成立,即:AB≠BA;(2)只有当矩阵A的列数与矩阵B的行数相等时,矩阵之积才有意义。
与“如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共...”考查相似的试题有:
- 设,且满足:,,求证:.
- 已知关于的不等式.(Ⅰ)当时,求此不等式的解集;(Ⅱ)若此不等式的解集为,求实数的取值范围.
- a、b为实数且a0,那么不等式中错误的是 ( )A.B.C.D.
- .不等式的解集为( )
- 已知a>b>0,给出下列四个不等式:①a2>b2;②2a>2b-1;③>-;④a3+b3>2a2b.其中一定成立的不等式为( )A.①②③B.①②④C.①③④D.②③④
- (本小题满分10分)选修4—5:不等式选讲设函数,(Ⅰ)若,解不等式;(Ⅱ)若函数有最小值,求实数的取值范围.
- 设a,b,c,d∈R,且a>b,c>d,则下列结论正确的是[ ]A.a+c>b+dB.a-c>b-dC.ac>bdD.
- 若正实数a,b,c满足b(a+b+c)+ac≥16,a+2b+c≤8,则a+2b+c的值为( )A.8B.6C.4D.2
- 在极坐标系中,过圆的圆心,且垂直于极轴的直线的极坐标方程为 .
- 在极坐标系中,两圆方程分别为ρ2-2ρcosθ+2=0,ρ=2sinθ,它们的位置关系是( ) A.相离 B.相交 C.内切 D.外切