本试题 “甲、乙、丙三名射箭运动员在某次测试中各射箭12次,三人的测试成绩如下表 甲的成绩 环数 7 8 9 10 频数 3 3 3 3 乙的成绩 环数 7 8 9 10 频数 4 2 2 4 丙的成...” 主要考查您对标准差、方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 标准差、方差
方差和标准差的定义:
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
设一组数据 的平均数为
的平均数为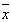 ,则
,则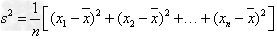 ,其中s2表示方差,s表示标准差。
,其中s2表示方差,s表示标准差。
一般地,平均数、方差、标准差具有如下性质:
若数据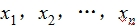 的平均数是
的平均数是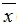 ,方差为s2,标准差为s.则新数据
,方差为s2,标准差为s.则新数据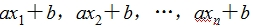 的平均数是a
的平均数是a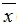 +b,方差为
+b,方差为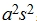 ,标准差为
,标准差为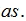
特别地,如a=1,则新数据的方差、标准差与原数据相同,分别为s2,s。因此,当一组数据均较大且接近某个常数时,可先将每个数同时减去这个常数,再计算这组新数据的方差,它与原数据的方差相等.
方差和标准差的意义:
方差和标准差都是用来描述一组数据波动情况的特征数,常数来比较两组数据的波动大小,方差较大的波动较大,方差较小的波动较小。
用样本的数字特征估计总体的数字特征分两类:
①用样本平均数估计总体平均数.
②用样本方差、标准差估计总体方差、标准差.样本容量越大,估计就越精确.
计算标准差的算法:
(1)算出样本数据的平均数;
(2)算出每个样本数据与样本平均数的差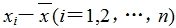 ;
;
(3)算出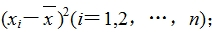
(4)算出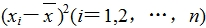 这n个数的平均数,即为样本方差s2;
这n个数的平均数,即为样本方差s2;
(5)算出方差的算术平方根,即为样本标准差s.
发现相似题
与“甲、乙、丙三名射箭运动员在某次测试中各射箭12次,三人的测...”考查相似的试题有:
- 甲,乙两个工人在同样的条件下生产,日产量相等,每天出废品的情况如下表所列,则有结论:[ ]A.甲的产品质量比乙的产品质量...
- 甲、乙两人5次射击命中的环数如下:甲:7 9 8 6 10;乙:7 8 9 8 8.则这两人5次射击命中的环数的平均数.x甲=.x乙=8,方差s甲...
- 下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:甲批次:0.598 0.625 0.628 0.595 0.639乙批次:0.618 ...
- 一组数据5,8,x,10,4的平均数是2x,则这组数据的方差是( ) A.6.8 B.6 C.7.8 D.8
- 随机抽取某中学甲、乙两班10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图。 (I)根据茎叶图判断哪个班...
- 下图是2009年举行的某次民族运动会上,七位评委为某民族舞蹈节日打出分数的茎叶图.去掉一个最高分和一个最低分后,所剩数据...
- 对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:甲273830373531乙332938342836...
- 以下茎叶图记录了甲、乙两组个四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙...
- 某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查...
- 下列说法中,正确的是( )A.频率分布直方图中各小长方形的面积不等于相应各组的频率B.一组数据的标准差是这组数据的方差的...